Expressões Numéricas: Guia Passo a Passo de Como Calcular

As expressões numéricas podem confundir muita gente.

Não é raro vermos na Internet desafios pedindo para dizer qual a opção correta com o valor de uma certa expressão numérica.

Isso porque, existe uma certa ordem de serem feitas as operações.

Calcular expressões numéricas exige a habilidade do uso de operações como adição, subtração, multiplicação, divisão, potenciação e radiciação.

E além disso, você precisa ter em mente qual ordem deve se seguida para calcular as operações.

Há ainda expressões mais complexas nas quais aparecem símbolos como parênteses, colchetes e chaves.

Além disso, você precisa ter em mente qual ordem deve ser seguida para calcular as operações e em qual símbolo se deve calcular primeiro.

Se você fica confuso na hora de saber qual operação fazer ou em qual símbolo se deve calcular primeiro, continue lendo para saber de uma vez por todas como fazer tudo isso.

O que são expressões numéricas?

Uma expressão numérica é uma sentença matemática que envolve somente números e uma ou mais operações.

As principais operações com as quais você vai lidar são:

• adição ($+$);
• subtração $(-)$;
• multiplicação($\times$);
• divisão($\div$);
• Potenciação;
• Radiciação.

Além dessas operações, há expressões que podem envolver frações e o valor absoluto.

Veja a seguir exemplos de expressões numéricas.

Exemplos

1. $12+3+2$
2. $15-3+1$
3. $2\times 3\div 6$
4. $13-2\times 4+6\div 2$
5. $2^2-3\times2+8\div 4-7$
6. $\sqrt{4\times12}+3+5$
7. $\dfrac{8-2}{16+8}$
8. $|-8+2\times(-5)|\div (-3)$

Lembrete: Jogo dos sinais

Antes de sabermos como calcular uma expressão numérica, vamos relembrar como fazer o jogo de sinais, uma vez que isso será feito várias vezes durante um cálculo.

Jogo dos sinais na multiplicação e na divisão

O jogo dos sinais na multiplicação segue as seguintes regras:

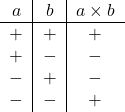
A tabela mostra como calcular o sinal do resultado quando multiplicamos dois números.

A primeira coluna mostra o sinal de um dos números, a segunda coluna mostra o sinal do outro e a terceira coluna nos dá o sinal do resultado.

Por exemplo, temos

• $3\times 4=12$;
• $3\times (-4)=-12$;
• $-3\times 4=-12$;
• $-3\times (-4)=12$.

O jogo de sinal na divisão é feito da mesma forma que na multiplicação, ou seja,

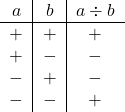
Jogo dos sinais na adição

Para a adição, temos três casos a considerar:

1. A adição de dois números positivos é um número positivo. Por exemplo, $$7+4=11.$$
2. A adição de dois números negativos é um número negativo. Por exemplo, $$(-3)+(-1)=-3-1=-4$$
3. A adição de dois números de sinais diferentes é feita seguindo a regra:

• subtrair os números e
• dar ao resultado o sinal daquele que possui o maior módulo.
  Por exemplo, $$(-10)+(+8)=-10+8=-2$$

Jogo dos sinais na subtração

Aqui você precisa usar os jogos de sinais da multiplicação e da adição.

A primeira coisa que precisa ser feita é eliminar os parênteses usando a jogo dos sinais da multiplicação.

Em seguida, basta proceder como no caso da adição.

Veja alguns exemplos para entender melhor.

Exemplo 1:

$(-3)-(-7)$

Solução

Aqui, o primeiro parênteses pode ser omitido, assim, $$(-3)-(-7)=-3-(-7).$$

Para omitir o outro, usamos a regra da multiplicação $(-)\times(-)=(+)$. Logo, $$-3-(-7)=-3+7.$$

Por fim, procedemos usando a regra da adição. Portanto, $$-3+7=4.$$

Exemplo 2:

$(-2)-(+7)$

Solução

Procedendo como antes, temos $$(-2)-(+7)=-2-7=-9.$$

Como calcular uma expressão numérica?

Agora que você já sabe o que é uma expressão numérica e relembrou os jogos de sinais, você está pronto para saber como calcular uma expressão numérica.

Para fazer esse cálculo você precisa ter em mente que existe uma ordem de prioridades das operações.

Continue lendo para saber que ordem é essa.

Símbolos de agrupamento

Primeiro de tudo você deve resolver as operações dentro dos símbolos de agrupamento, caso apareçam.

Os principais símbolos de agrupamento são:

• parênteses $(\;)$;
• colchetes $[\;]$;
• chaves ${\;}$

Se em uma expressão numérica aparecer os três símbolos acima, então você deverá resolver primeiro as operações entre parênteses, em seguida as que estão entre colchetes, e por fim, as que estão entre chaves.

Ordem das operações

Dentre as operações, a ordem em que se devem fazê-las é a seguinte:

• Potênciação e radiciação: resolva primeiro as potências e raízes na ordem em que você desejar, pois não há prioridades entre essas duas operações.
• Multiplicação e divisão: em segundo lugar, quando não houver mais potências e raízes, resolva as multiplicações e divisões da esquerda para a direita.
• Adição e subtração: Finalmente, realize as somas e as subtrações da esquerda para a direita.

10 exemplos de expressões numéricas calculadas

Exemplo 1: $-5-10+3-4$

Solução

Observe que essa expressão só contém as operações de adição e subtração.

Assim, vamos calculá-la, fazendo as contas da esquerda para a direita.

\begin{eqnarray*}
-5-10+3-4&=&-15+3-4\\
&=&-12-4\\
&=&-16
\end{eqnarray*}

Exemplo 2: $28\div 7\times 4\div 2$

Solução

Essa expressão contém somente operações de multiplicação e divisão.

Logo, calculando da esquerda para a direita, obtemos

\begin{eqnarray*}
28\div 7\times 4\div 2&=& 4\times 4\div 2\\
&=& 16\div 2\\
&=& 8
\end{eqnarray*}

Exemplo 3: $18+36\div 9\times 2$

Solução

Lembrando das prioridades, devemos calcular primeiro a multiplicação e a divisão.

\begin{eqnarray*}
18+36\div 9\times 2&=&18+4\times 2\\
&=&18+8\\
&=&26
\end{eqnarray*}

Exemplo 4: $75\div(-5)\times 3+4$

Solução

Seguindo a ordem das operações e lembrado do jogo de sinais, temos

\begin{eqnarray*}
75\div(-5)\times 3+4&=&-15\times 3+4\\
&=&-45+4\\
&=& -41
\end{eqnarray*}

Exemplo 5: $56\div 2^3\times 20$

Solução

Primeiro vamos resolver a potenciação.

$$56\div 2^3\times 20=56\div 8\times 20$$

Agora, vamos resolver a divisão e a multiplicação da esquerda para a direita.

\begin{eqnarray*}
56\div 8 \times&=&7\times 20\\
&=& 140
\end{eqnarray*}

Exemplo 6: $\sqrt{4\times 9}\div 2+4$

Solução

Primeiro, resolvemos a raiz quadrada.

\begin{eqnarray*}
\sqrt{4\times 9}\div 2+4&=&\sqrt{36}\div 2+4\\\\
&=&6\div 2+4
\end{eqnarray*}

Em seguida, resolvemos a divisão: $$6\div2+4=3+4.$$

E por fim, a soma, $$3+4=7.$$

Exemplo 7: $(11-3)^2\div (6^2-4)$

Solução

Vamos começar calculando as expressões dentro de cada um dos parênteses obedecendo a ordem de prioridade da operações.

\begin{eqnarray*}
(11-3)^2\div ( 6 ^2-4)&=&8 ^2\div (6 ^2-4)\\\\
&=&8^2\div (36-4)\\\\
&=&8^2\div 32 \\\\
\end{eqnarray*}

E em seguida calcule a potência e, por fim, a divisão.
$$8^2\div 32=64\div32=2.$$

Exemplo 8: $4+{[(5-1)\times 7]\div14}$.

Solução

Primeiro vamos resolver a expressão entre parênteses. $$4+{[(5-1)\times 7]\div14}=4+{[4\times7]\div14}.$$

Em segundo lugar, resolvemos a expressão entre colchetes.$$4+{[4\times7]\div14}=4+{28\div14}$$

Por fim, resolvemos a expressão entre chaves e a última soma obtendo $$4+{28\div14}=4+2=6.$$

Exemplo 9: $\dfrac{\sqrt{2^5-(-4)}}{[12-(1-7)]\div 6}$

Solução

Vamos começar calculando a expressão no numerador:

\begin{eqnarray*}
&&\frac{\sqrt{2^5-(-4)}}{[12-(1-7)]\div 6}\\
&=&\frac{\sqrt{32-(-4)}}{[12-(1-7)]\div 6}\\
&=&\frac{\sqrt{36}}{[12-(1-7)]\div 6}\\
&=&\frac{6}{[12-(1-7)]\div 6}
\end{eqnarray*}

Agora vamos calcular a expressão no denominador

\begin{eqnarray*}
&=&\frac{6}{[12-(-6)]\div 6}\\
&=&\frac{6}{18\div 6}\\
&=&\frac{6}{3}=2
\end{eqnarray*}

Exemplo 10: $|-8+2\times (-5)|\div (-3)$

Solução

Vamos calcular primeiro dentro do valor absoluto.

\begin{eqnarray*}
|-8+2\times (-5)|\div (-3)&=& |-8-10|\div(-3)\\
&=&|-18|\div (-3)\\
\end{eqnarray*}

Agora calcule o valor absoluto e a divisão $$18\div (-3)=-6.$$

04 Problemas de Concursos Públicos sobre Expressões Numéricas

Problema 1

FGV – 2018 – BANESTES (Banco) – Técnico em Segurança do Trabalho

O resultado da operação $5 + 3 × 7-4$ é:

a) 14;
b) 22;
c) 24;
d) 28;
e) 52.

Solução
Essa expressão numérica contém as operações de adição, subtração e multiplicação.

A prioridade é resolver a multiplicação primeiro. Assim, temos $$5+3\times7-4=5+21-4.$$

Agora que restaram apenas a adição e a subtração, calculamos a expressão da esquerda para a direita. Dessa forma, $$5+21-4=26-4=22.$$

Portanto, a alternativa correta é a b).

Problema 2

Prova OBJETIVA – 2015 – Prefeitura de Tramandaí – RS – Auxiliar Legislativo

Dadas as três expressões numéricas abaixo, é CORRETO afirmar que:

a) $2 + [(5 – 3) + 4] \times 2 + 3$

b) $13 – [5 \times (2 – 1) + 4 \times 2]$

c) $6 + 4 \times 2 \times (5 – 1) – 7$

A) $b < a < c$

B) $a < b < c$

C) $c < a < b$

D) $c < b < a$

Solução:

Vamos calcular cada uma das expressões.

Seguindo as ordens dos símbolos e das operações vistas acima, temos

a)

\begin{eqnarray*}
2 + [(5 – 3) + 4] \times 2 + 3&=&2+[2+4]\times 2+3\\
&=&2+6\times 2+3\\
&=&2+12+3\\
&=&17
\end{eqnarray*}

b)

\begin{eqnarray*}
13 – [5 \times (2 – 1) + 4 \times 2]&=&13-[5\times 1+4\times 2]\\
&=&13-[5+4\times2]\\
&=&13-[5+8]\\
&=&13-13\\
&=& 0
\end{eqnarray*}

c)

\begin{eqnarray*}
6 + 4 \times 2 \times (5 – 1) – 7&=&6+4\times 2\times 4 -7\\
&=&6+8\times 4-7\\
&=&6+32-7\\
&=&38-7\\
&=&31
\end{eqnarray*}

Logo, $$b<a<c,$$ e, por isso, a resposta correta é a $A)$

Problema 3

EXCELÊNCIA – 2018 – Prefeitura de Coroados – SP – Agente Comunitário de Saúde

A expressão numérica $${– 72: (– 4 + 3) – [– 3 \times (– 2 + 3 – 1)^2 – 18 : (– 1 + 4)^2] }$$ é igual a:

a) 54
b) 74
c) 84
d) Nenhuma das alternativas

Solução

Vamos resolver primeiro as expressões dentro dos parênteses.

${– 72: (– 4 + 3) – [– 3 \times (– 2 + 3 – 1)^2 – 18 : (– 1 + 4)^2] }$
$=-72:(-1)-[-3\times 0^2-18:3^2]$

Agora vamos resolver a expressão entre colchetes.
$=-72:(-1)-[-3\times 0-18:9]$
$=-72:(-1)-[0-18:9]$
$=-72:(-1)-[0-2]$
$=-72:(-1)-(-2)$

Finalmente, resolvemos a divisão e em seguida a subtração.

$$=72-(-2)=72+2=74.$$

Problema 4

FCC – 2018 – SABESP – Atendente a Clientes

Dez amigos decidiram viajar por 5 dias e se reuniram para fazer o planejamento das despesas. Após pesquisar, optaram por alugar um chalé grande o suficiente para comportá-los, por um total de R$ 12.370,00 pelos 5 dias de estadia. Dois dias antes da viagem, porém, um dos amigos teve um imprevisto e comunicou que não poderia viajar. Como o chalé já estava alugado, os outros amigos tiveram de arcar com um custo adicional. A expressão numérica que melhor representa o custo adicional de estadia é

a) $\dfrac{12.370}{9}-\dfrac{12.370}{10}$

b) $\dfrac{12.370}{10}-\dfrac{12.370}{9}$

c) $\dfrac{12.370}{10}\div 5$

d) $\dfrac{12.370}{10}$

e) $\dfrac{12.370}{9}$

Solução

O custo para cada um dos 10 amigos seria de $$\frac{12.370}{10}.$$

Com a desistência de um amigo o custo para cada um será de $$\frac{12.370}{9}.$$

Com isso, cada um desses terá um custo adicional de $$\frac{12.370}{9}-\frac{12.370}{10}.$$

Portanto, a alternativa correta é a)

Conclusão

As expressões numéricas estão presentes em vários lugares esperando alguém para calculá-las.

E vimos nesse artigo como se deve fazer esse cálculo. Vamos relembrar a ordem em que as operações devem ser feitas.

Você deve resolver primeiro as expressões nos símbolos de agrupamento sempre obedecendo a seguinte ordem de prioridade:

• potenciação e radiciação;
• multiplicação e divisão (da esquerda para a direita);
• adição e subtração (da esquerda para a direita).

Agora em só colocar o que você viu aqui em prática.

Com passar do tempo, você vai conseguir calcular expressões numéricas cada vez mais rápido.

Gostou do conteúdo? Aproveite e conheça o curso Matemática ZERO 2.0 e fortaleça a sua base matemática.