Frações são representações matemáticas de partes de um todo. Expressas na forma de $\dfrac{a}{b}$, onde $a$ é o numerador (parte) e $b$ é o denominador (todo), elas indicam a divisão de um objeto em partes iguais.
Quando se trata de matemática, frações são um dos conceitos fundamentais que todos nós encontramos em algum momento de nossas vidas.
Você já dividiu uma pizza com amigos e teve que descobrir quanto cada um iria receber?

Ou talvez tenha se deparado com uma receita que pedia $\dfrac{3}{4}$ de xícara de açúcar?
Se você respondeu sim a qualquer uma dessas perguntas, então você já tem uma noção da presença das frações no nosso dia a dia.
O que são frações
Em termos simples, frações são uma forma de representar partes de um todo ou de uma coleção de objetos.
A forma mais comum de representar uma fração é $\dfrac{a}{b}$.
O número $a$ é chamado de numerador e representa a quantidade de partes iguais do todo ou da coleção que são consideradas.
Já o número $b$ é chamado de denominador e representa o número total de partes iguais em que o todo é dividido ou o número total dos mesmos objetos em uma coleção.
Por exemplo, se uma pizza é dividida em 8 fatias iguais e você pega 3 desses pedaços, então a fração que representa essa parte é $\dfrac{3}{8}$.
Nesse caso, o numerador é 3 (indicando que você pegou 3 pedaços) e o denominador é 8 (indicando que a pizza foi dividida em 8 partes iguais).
Por que as frações são importantes na matemática?
As frações desempenham um papel fundamental na matemática e em muitos aspectos da vida cotidiana.
Elas são usadas em uma variedade de situações, desde a cozinha até a construção civil.
Veja a seguir algumas razões pelas quais as frações são importantes:
- Medição precisa: Elas são usadas com frequência para representar medidas precisas, como metades, terços e quartos, que são essenciais em ciências, engenharia e construção.
- Compreensão de proporções: Elas são a base para entender proporções e porcentagens, conceitos fundamentais em matemática e estatística.
- Resolução de problemas: Muitos problemas do mundo real envolvem frações, e saber como trabalhar com elas é essencial para resolvê-los de forma eficaz.
O objetivo desse artigo é apresentar não só o básico sobre frações, mas também como realizar operações com elas, como soma, subtração, multiplicação e divisão.
Como Somar Frações
A primeira operação que vamos mostrar é a adição de frações.
Para fazer isso, temos dois casos a considerar:
- frações com mesmo denominador
- frações com denominadores diferentes.
Passos para somar frações com o mesmo denominador.
Quando você soma duas ou mais frações com o mesmo denominador, você basicamente está combinando partes iguais.
Voltando para o exemplo da pizza, se você pega duas fatias e em seguida pega mais uma, você fica com três fatias. Ou seja, $$\frac{2}{8}+\frac{1}{8}=\frac{3}{8}.$$
Veja a seguir um passo a passo para somar frações com o mesmo denominador:
- Certifique-se que as frações possuem denominadores iguais.
- Some os numeradores
- Repita o denominador
Exemplo 1: $$\dfrac{2}{7}+\dfrac{4}{7}=\frac{2+4}{7}=\frac{6}{7}.$$
Exemplo 2: $$\frac{17}{5}+\frac{6}{5}=\frac{17+6}{5}=\frac{23}{5}.$$
Passos para Somar Frações com Denominadores Diferentes
Vejamos agora como somar frações com denominadores diferentes:
- Encontre o denominador comum: O primeiro passo é identificar um denominador comum para todas as frações envolvidas.
Isso significa encontrar um número que seja divisível por todos os denominadores originais. Para encontrar esse número, basta calcular o mínimo múltiplo comum (mmc). - Converta as frações: Agora, é preciso expressar todas as frações com o mesmo denominador encontrado no passo anterior.
Para fazer isso, você multiplica tanto o numerador quanto o denominador de cada fração pelo fator necessário para que o denominador se torne igual ao denominador comum. - Some as frações com os denominadores iguais: Faça isso usando o passo a passo mostrado acima.
Exemplo 3: $\dfrac{1}{3}+\dfrac{1}{4}$
Solução: O primeiro passo é determinar o mínimo múltiplo comum de 3 e 4, que é 12.
Em seguida, precisamos expressar ambas as frações com denominador 12:
$$\frac{1}{3}=\frac{4}{12}\quad{\rm e}\quad \frac{1}{4}=\frac{3}{12}.$$
Note que na primeira frações multiplicamos o numerador e o denominador por 4 e na segunda, multiplicamos por 3.
Agora, somamos como antes: $$\frac{1}{3}+\frac{1}{4}=\frac{4}{12}+\frac{3}{12}=\frac{4+3}{12}=\frac{7}{12}.$$
Observação: Há situações podemos simplificar a fração resultante, ou seja, dividir tanto o numerador quanto o denominador pelo seu máximo divisor comum (mdc). Por exemplo, $$\frac{8}{15}+\frac{2}{15}=\frac{10}{15}=\frac{2}{3}.$$ Aqui dividimos o numerador e o denominador por 5, que é o mdc de 10 e 15.
Como Subtrair
Para subtrair frações procedemos de modo que na adição.
No caso em que os denominadores são iguais, subtrai-se os numeradores e repete-se o denominador.
Exemplo 4: $$\frac{8}{9}-\frac{4}{9}=\frac{4}{9}.$$
E no caso em os denominadores são diferentes, encontramos o denominador comum.
Em seguida, encontramos as frações com o denominador encontrado que são equivalentes às frações originais.
E, por fim, efetuamos a subtração.
Exemplo 5: $$\frac{15}{11}-\frac{4}{3}=\frac{45}{33}-\frac{44}{33}=\frac{45-44}{33}=\frac{1}{33}.$$
Como Multiplicar
Para multiplicar frações, você está essencialmente calculando uma parte de uma parte.
Em outras palavras, você está encontrando a fração de uma fração. Para fazer isso, siga esses passos simples:
- Multiplique os numeradores: Comece multiplicando os numeradores (os números de cima) das duas frações. Isso lhe dará o numerador do resultado.
- Multiplique os denominadores: Em seguida, multiplique os denominadores (os números de baixo) das duas frações. Isso lhe dará o denominador do resultado.
- Simplifique, se necessário: Simplifique a fração resultante, se possível, dividindo o numerador e o denominador pelo seu maior divisor comum.
Exemplo 6: Calcule $$\frac{7}{8}\cdot \frac{3}{5}.$$
Solução: Seguindo os passos acima, temos $$\frac{7}{8}\cdot\frac{3}{5}=\frac{7\cdot 3}{8\cdot 5}=\frac{21}{40}.$$
Exemplo 7: Calcule $$\frac{6}{7}\cdot\frac{2}{3}.$$
Solução: Temos $$\frac{6}{7}\cdot\frac{2}{3}=\frac{6\cdot 2}{7\cdot 3}=\frac{12}{21}=\frac{4}{7}.$$
Como dividir
Para efetuar uma divisão de frações, siga os seguintes passos:
- Multiplique a primeira fração pelo o inverso (recíproco) da segunda. Lembre-se que para inverter uma fração basta trocar o numerador pelo denominador e vice-versa.
- Efetue a multiplicação, procedendo como no passo a passo acima.
Exemplo 8: Calcule \[\frac{3}{4}\div \frac{2}{5}.\]
Solução: Temos \[\frac{3}{4}\div \frac{2}{5}=\frac{3}{4}\cdot \frac{5}{2}=\frac{15}{8}.\]
Resolvendo Problemas com Frações
Agora que você já aprendeu como somar, subtrair, multiplicar e dividir frações, é hora de aplicar esses conhecimentos para resolver problemas do dia a dia que envolvem esse assunto.
Problema 1
Alex recebeu um vale-presente de R\$ 600,00 em seu aniversário. Ele usou $\dfrac{1}{5}$ para comprar um videogame e $\dfrac{1}{8}$ para comprar uma camiseta nova. Que fração do vale-presente Alex gastou?
Solução:
Para saber qual fração do vale-presente Alex gastou, precisamos somar as frações que representam os valores que ele gastou no videogame e na camiseta:
- Alex gastou $\dfrac{1}{5}$ do vale-presente em um videogame e
- Alex gastou $\dfrac{1}{8}$ do vale-presente em uma camiseta nova.
Para encontrar a fração total que ele gastou, precisamos somar essas duas frações:
$$\frac{1}{5} + \frac{1}{8}$$
Para adicionar essas frações, precisamos de um denominador comum. O mínimo múltiplo comum de 5 e 8 é 40, então podemos reescrever as frações com denominador comum de 40:
$$\frac{8}{40} + \frac{5}{40}$$
Agora que as frações têm o mesmo denominador, podemos somá-las:
$$\frac{8}{40} + \frac{5}{40} = \frac{8 + 5}{40} = \frac{13}{40}$$
Então, Alex gastou $\dfrac{13}{40}$ do vale-presente de R\$ 600,00.
Problema 2
Em uma partida de futebol, o Jogador A percorre $\dfrac{3}{5}$ do comprimento do campo, enquanto o Jogador B percorre $\dfrac{7}{8}$ do mesmo comprimento. Quanto o Jogador B percorreu a mais do que o Jogador A?
Solução:
Para resolver esse problema, podemos subtrair a distância percorrida pelo Jogador A da distância percorrida pelo Jogador B:
Distância percorrida pelo Jogador B – Distância percorrida pelo Jogador A
=$\dfrac{7}{8}-\dfrac{3}{5}$
Para subtrair, precisamos de um denominador comum, que é 40.
Temos que \[\frac{7}{8}=\frac{35}{40}\quad\mbox{e}\quad \frac{3}{5}=\frac{24}{40}.\]
Agora, podemos calcular:
$$\frac{35}{40}-\frac{24}{40}=\frac{35-24}{40}=\frac{11}{40}.$$
Portanto, o Jogador B avançou $\dfrac{11}{40}$ do comprimento do campo a mais do que o Jogador A.
Problema 3
Em um baralho de cartas, $\frac{1}{2}$ das cartas são vermelhas. Das cartas vermelhas, $\frac{3}{4}$ são de copas. Qual fração do baralho consiste as cartas de copas?
Solução:
Para encontrar a fração do baralho que consiste de cartas de copas, multiplicamos a fração de cartas vermelhas pela fração de copas entre as cartas vermelhas:
$$\frac{1}{2} \cdot \frac{3}{4} = \frac{1 \cdot 3}{2 \cdot 4} = \frac{3}{8}$$
Portanto, a fração do baralho que consiste de cartas de copas é $\frac{3}{8}$.
Problema 4
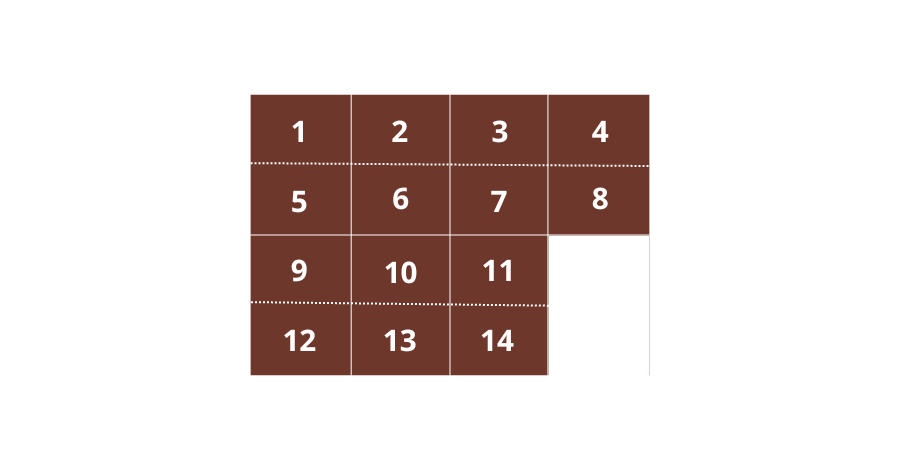
Pedro tem uma barra de chocolate que pesa $\frac{7}{8}$ kg. Se ele quebrar a barra em pedaços de $\frac{1}{16}$ kg cada, quantos pedaços de chocolate ele terá?
Solução:
Para resolver esse problema, precisamos dividir o peso da barra de chocolate pelo peso de cada pedaço:
$$\frac{7}{8}\div\frac{1}{16}.$$
Para calcular essa divisão, multiplicamos a primeira fração pelo inverso da segunda:
\[\frac{7}{8}\cdot\frac{16}{1}=\frac{7\cdot 16}{8\cdot 1}=\frac{112}{8}=14\]
Portanto, Pedro terá 14 pedaços de chocolate.
Ilustramos a situação com a figura abaixo:
Gostou desse conteúdo da matemática básica? Aproveite e conheça o curso Matemática ZERO 2.0 e fortaleça a sua base matemática.


0 Comentários