O Teorema Fundamental do Cálculo (TFC) é uma pedra angular no estudo do cálculo e das operações fundamentais de derivação e integração.
Dividido em duas partes complementares, esse teorema estabelece uma relação fundamental entre as operações de integração e diferenciação.
A Parte I do TFC descreve a conexão entre a integral definida e as funções primitivas, fornecendo um método sistemático para calcular áreas sob curvas e quantidades acumuladas ao longo de intervalos.
Por outro lado, a Parte II demonstra a relação entre a derivada e a integral de uma função, revelando a inversão dessas operações.
Neste artigo, apresentaremos os enunciados e as demonstrações das duas partes desse teorema.
Integral definida
Antes de enunciarmos o Teorema Fundamental do Cálculo, vamos entender primeiro o que é a integral definida.
Seja $f:[a,b]\to\mathbb{R}$ uma função contínua.
Vamos dividir $[a,b]$ em $n$ subintervalos de comprimentos iguais a $\Delta x=\dfrac{b-a}{n}$ que se interceptam somente nos extremos.
Para isso, considere os pontos $$a=x_0<x_1<x_2<\ldots<x_{n-1}<x_n=b.$$Em cada subintervalo $[x_{k-1}, x_k]$ escolha um ponto arbitrário $x_k^{\ast}$ e considere a soma $$S_n:=\sum_{k=1}^nf(x_k^{\ast})\Delta x$$
A integral definida de $f$ sobre $[a,b]$ é $$\int_a^bf(x)\;dx=\lim_{n\to \infty} S_n.$$
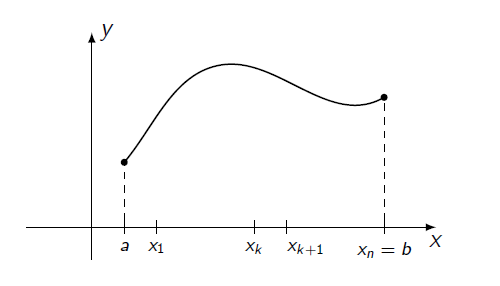
Definimos ainda $$\int_a^af(x)\;dx=0\quad\mbox{e}\quad\int_b^af(x)\;dx=-\int_a^bf(x)\;dx.$$
Teorema Fundamental do Cálculo – Parte I
Teorema: Se $f$ é contínua em $[a,b]$ e $F:[a,b]\to \mathbb{R}$ é uma função contínua tal que $F'(x)=f(x)$ para todo $x\in (a,b)$, então $$\int_a^bf(x)\;dx=F(b)-F(a).$$
Demonstração: Dada uma partição de $P$ de $[a,b]$: $$P:x_0=a<x_1<x_2<\cdots<x_n=b, $$ podemos escrever $F(b)-F(a)$ da seguinte forma:
$$\begin{eqnarray*}F(b)-F(a)&=&(F(x_1)-F(a))+(F(x_2)-F(x_1))+\cdots+(F(b)-F(x_{n-1}))\\&=& \sum_{i=1}^n(F(x_i)-F(x_{i-1}))\end{eqnarray*}$$
Pelo Teorema do Valor Médio, existe um $x_i^{\ast}$ em $[x_{i-1}, x_i]$, tal que $$F(x_i)-F(x_{i-1})=F'(x_i^{\ast})(x_i-x_{i-1})=f(x_i^{\ast})(x_i-x_{i-1})=f(x_i^{\ast})\Delta x_i.$$
Com isso, temos $$F(b)-F(a)=\sum_{i=1}^nf(x_i^{\ast})\Delta x_i.$$
Tomando o limite com $n\to\infty$ chegamos a $$F(b)-F(a)=\lim_{n\to\infty}\sum_{i=1}^nf(x_i^{\ast})\Delta x_i=\int_a^bf(x)\;dx,$$
como queríamos demonstrar.
Notação: A diferença $F(b)-F(a)$ é denotada por $F(x)\Big|_a^b$.
Exemplo: Considere $f(x)=2x+\cos x$ e a integral definida dada por $$\int_0^{\pi/6}f(x)\;dx=\int_0^{\pi/6}(2x+\cos x)\;dx.$$
Uma vez que a função $F(x)=x^2+\mbox{sen}\;x$ é contínua e satisfaz $$F'(x)=2x+\cos x=f(x),$$ para todo $x\in (0,\pi/6$)$ temos pela Parte I do Teorema Fundamental do Cálculo que
$$\begin{eqnarray*}\int_0^{\pi/6}(2x+\cos x)\;dx&=&F(\pi/6)-F(0)\\&=&\frac{\pi^2}{36}+\mbox{sen}\left(\frac{\pi}{6}\right)-(0+\mbox{sen}\;0)\\&=& \frac{\pi^2}{36}+\frac{1}{2}.\end{eqnarray*}$$
Teorema Fundamental do Cálculo – Parte II
Teorema: Suponha que $f:[a,b]\to\mathbb{R}$ seja uma função contínua e defina $$g(x)=\int_a^xf(t)\;dt,\qquad x\in[a,b].$$
Então $g$ é uma função contínua, derivável em $(a,b)$ e $$g'(x)=f(x), \quad x\in (a,b).$$
Demonstração: Sejam $x\in (a,b)$ e $h>0$ pequeno de tal forma que $x+h\in(a,b)$. Temos que $$g(x+h)-g(x)=\int_a^{x+h}f(t)\;dt-\int_a^xf(t)\;dt=\int_x^{x+h}f(t)\;dt.$$
Por outro lado, sejam $m(h)$ e $M(h)$ os valores mínimo e máximo de $f$ em $[x, x+h]$, respectivamente. Dessa forma, tem-se que $$hm(h)\leq \int_x^{x+h}f(t)\;dt\leq hM(h), $$ ou seja, $$m(h)\leq \frac{1}{h}\int_x^{x+h}f(t)\;dt\leq M(h).$$
Se $x_m$ e $x_M$ são os pontos de mínimo e de máximo em $[x,x+h]$, então segue pelo Teorema do Valor Intermediário que existe um $c_h$ entre $x_m$ e $x_M$ tal que $$f(c_h)=\frac{1}{h}\int_x^{x+h}f(t)\;dt.$$
Portanto, $$\frac{g(x+h)-g(x)}{h}=f(c_h).$$
Agora, temos que $h\to 0^{+}$ (lembre-se que estamos assumindo $h>0$) implica que $c_h\to x$ e, por isso, $$\lim_{h\to 0^{+}} f(c_h)=f(x),$$ pois $f$ é contínua.
Logo, $$\lim_{h\to 0^{+}} \frac{g(x+h)-g(x)}{h}=\lim_{h\to 0^{+}}f(c_h)=f(x).$$
Por um argumento similar, mostra-se $$\lim_{h\to 0^{-}} \frac{g(x+h)-g(x)}{h}=f(x).$$
Portanto, $g$ é diferenciável em $(a,b$) com $g'(x)=f(x)$. Além disso, a continuidade de $g$ nos extremos $x=a$ e $x=b$ é uma consequência da existência dos limites laterais acima.
A prova está completa.
Exemplo: Para $g(x)=\displaystyle\int_{-5}^{x}e^{t^4}\;dt$, calcule $g'(1)$.
Solução.
Pela Parte II do Teorema Fundamental do Cálculo, temos $$g'(x)=e^{x^4}.$$ Daí, segue que $g'(1)=e$.
Conclusão
O Teorema Fundamental do Cálculo emerge como um alicerce crucial no estudo do cálculo diferencial e integral, estabelecendo uma conexão profunda entre as operações de derivada e integral.
As duas partes distintas deste teorema desvendam a relação intrínseca entre integrais definidas, funções primitivas e as operações de diferenciação.
Se você ficou com alguma dúvida com relação a esse conteúdo, não hesite em deixar um comentário abaixo.




0 Comentários