A matemática é uma linguagem universal que nos permite decifrar os segredos do mundo ao nosso redor.
Ela desvenda padrões ocultos, resolve enigmas complexos e fornece as ferramentas necessárias para entender fenômenos naturais, construir edifícios impressionantes, projetar circuitos elétricos e até mesmo navegar pelos oceanos.
E no cerne da matemática, encontramos o Teorema de Pitágoras, uma das descobertas mais notáveis da história da geometria.
A seguir, você vai conhecer uma elegante relação entre os comprimentos dos lados de um triângulo retângulo que pode ser demonstrada de muitas maneiras e que tem uma variedade de aplicações na matemática.
Espero que você tenha uma boa leitura.
Fundamentos da Geometria
A geometria é uma das áreas mais antigas e fundamentais da matemática, preocupada com o estudo de formas, tamanhos, medidas e propriedades dos objetos espaciais.
Antes de nos aprofundarmos no Teorema de Pitágoras, é importante estabelecer alguns conceitos básicos que servirão como alicerce para o nosso entendimento.
Triângulos e suas Classificações
Um triângulo é uma figura geométrica composta por três lados e três ângulos.
No contexto do Teorema de Pitágoras, os triângulos retângulos desempenham um papel central.
Eles são triângulos que possuem um ângulo reto, ou seja, um ângulo de $90º$. Os outros dois ângulos agudos (menores que $90°$) são complementares, somando sempre $90°$
Além dos triângulos retângulos, há outras classificações importantes, como os triângulos equiláteros (todos os lados e ângulos iguais), os triângulos isósceles (dois lados e ângulos iguais) e os triângulos escalenos (todos os lados e ângulos diferentes).
No entanto, para compreender plenamente o Teorema de Pitágoras, é crucial concentrar-se nos triângulos retângulos.
Medida de Ângulos e Lados
A medida de ângulos em graus é uma parte fundamental da geometria.
Um círculo completo é dividido em $360°$, e os ângulos são usados para determinar rotações, direções e inclinações.
No caso dos triângulos retângulos, o ângulo reto sempre mede $90°$, enquanto os outros dois ângulos agudos somam 90 graus, como mencionado anteriormente.
Além dos ângulos, a medida dos lados dos triângulos também desempenha um papel essencial.
O comprimento dos lados é frequentemente representado por letras minúsculas, como $a, b$, e $c$, onde $a$ é a hipotenusa (o lado oposto ao ângulo reto) e $b$ e $c$ são os catetos (os lados que formam o ângulo reto).
Teorema de Pitágoras e Triângulos Retângulos
Agora que estabelecemos a base, podemos introduzir o Teorema de Pitágoras.
Este teorema afirma que, em um triângulo retângulo, o quadrado da medida da hipotenusa ($a$) é igual à soma dos quadrados das medidas dos catetos ($b$ e $c$).
Matematicamente, isso pode ser expresso como:
\[a^2=b^2+c^2\]
Essa relação fundamental entre os lados de um triângulo retângulo é a base para calcular distâncias, resolver problemas de geometria e tem aplicações em várias áreas da matemática e ciências naturais.
Com essa compreensão dos conceitos básicos da geometria, estamos agora preparados para explorar mais profundamente o Teorema de Pitágoras e suas aplicações práticas.
O Teorema de Pitágoras em Detalhes
O Teorema de Pitágoras é uma pedra angular da geometria e da matemática, que desempenha um papel fundamental na compreensão das relações entre os lados de um triângulo retângulo.
Este teorema afirma o seguinte:
“Em um triângulo retângulo, o quadrado da medida da hipotenusa é igual à soma dos quadrados das medidas dos catetos.”
Em termos mais simples, se você tem um triângulo com um ângulo reto (90 graus), então a soma dos quadrados das medidas dos dois lados mais curtos (os catetos) é igual ao quadrado da medida do lado mais longo (a hipotenusa).
A Fórmula do Teorema de Pitágoras
A expressão matemática do Teorema de Pitágoras é a seguinte: \[a^2=b^2+c^2\]
Onde:
- $a$ representa o comprimento da hipotenusa.
- $b$ e $c$ representam os comprimentos dos catetos.
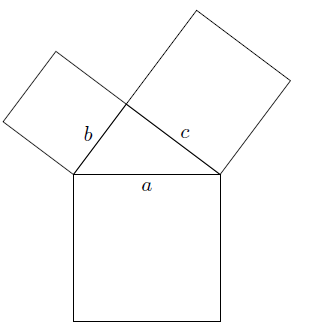
Observando a figura acima, concluímos do Teorema de Pitágoras que a área do quadrado de lado $a$ é igual à soma das áreas dos quadrados de lados $b$ e $c$
Demonstração do Teorema de Pitágoras
Há várias maneiras de provar o Teorema de Pitágoras, incluindo demonstrações geométricas, demonstrações algébricas e argumentos de similaridade de triângulos.
A demonstração que mostraremos é devido James A. Garfield (1831-1881).
Garfield foi o 20° presidente dos Estados Unidos.
Antes de ser presidente, ele foi congressista republicano de Ohio de 1862 a 1880.
Enquanto servia no Congresso dos EUA, Garfield deu uma demonstrações mais interessantes do Teorema de Pitágoras já criadas.
Ela é baseada na figura a seguir.

A área de um trapézio de bases $b$ e $c$ e altura $b+c$ é \[A=\frac{(b+c)(b+c)}{2}.\]
Por outro lado, como você pode ver na figura, a área é igual à soma das áreas de três triângulos retângulos.
Assim, \[\frac{(b+c)^2}{2}=\frac{bc}{2}+\frac{bc}{2}+\frac{a^2}{2}.\]
Daí, temos que \[\frac{b^2}{2}+\frac{c^2}{2}+bc=bc+\frac{a^2}{2},\] o que implica que \[a^2=b^2+c^2.\]
02 aplicações do Teorema de Pitágoras
Apresentaremos duas situações onde podemos aplicar o Teorema de Pitágoras.
Diagonal de um quadrado
A primeira aplicação é no cálculo do comprimento da diagonal de um quadrado.
Seja $ABCD$ um quadrado com lado medindo $\ell$. Trace a diagonal $AC$ e denote o seu comprimento por $d$.
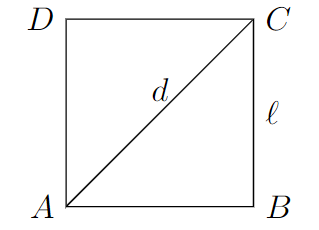
Aplicando o teorema ao triângulo $ABC$, temos \[d^2=\ell^2+\ell^2\Rightarrow d^2=2\ell^2\Rightarrow d=\ell\sqrt{2}.\]
Altura de um triângulo equilátero
Uma outra aplicação é para calcular a medida da altura de um triângulo equilátero.
Sejam $ABC$ um triângulo equilátero de lado de comprimento $\ell$ e $H$ o ponto médio do segmento $BC$.
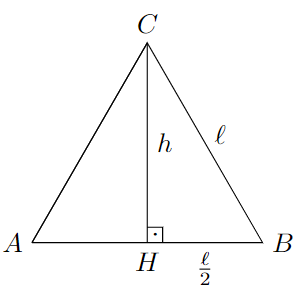
Seja $h$ o comprimento da altura $AH$. Vamos usar o teorema de Pitágoras para calcular $h$ em função do lado do triângulo.
Para isso, considere o triângulo retângulo $CHB$. Pelo teorema de Pitágoras temos
\begin{eqnarray*}
\ell^2&=&\left(\frac{\ell}{2}\right)^2+h^2\Rightarrow\\ \Rightarrow h^2&=&\frac{3\ell^2}{4} \Rightarrow\\ \Rightarrow h&=&\frac{\ell\sqrt{3}}{2}.
\end{eqnarray*}
Conclusão
Neste artigo, discorremos um pouco sobre um dos Teoremas mais famosos da matemática.
Tal popularidade é demonstrada por suas centenas de provas, dentre elas a de um presidente dos Estados Unidos.
Além disso, na matemática, você se deparará com várias aplicações desse teorema fantástico.
Tudo isso mostra a grande importância que o Teorema de Pitágoras tem ao longo da história.
E você?
Já teve que usar o Teorema de Pitágoras alguma vez?
0 Comentários