Você já parou para observar a beleza da natureza e notou padrões matemáticos intrincados (como a sequência de Fibonacci) que a governam?
Imagine, por um momento, as espirais perfeitas das conchas, as pétalas harmoniosas de uma flor ou até mesmo as galáxias em expansão no cosmos.
Há uma força matemática por trás de todos esses fenômenos, e ela é conhecida como a “sequência de Fibonacci.”
A matemática é uma linguagem universal que se entrelaça com o mundo que nos rodeia de maneiras fascinantes e inesperadas.
A sequência de Fibonacci é um dos exemplos mais cativantes dessa conexão, evocando curiosidade e admiradores ao longo da história.
Este artigo o levará a uma jornada pela mágica matemática por trás dessa sequência aparentemente simples, revelando suas origens históricas, propriedades matemáticas intrigantes e uma miríade de aplicações surpreendentes.
Aqui, você descobrirá que a sequência de Fibonacci não é apenas uma sequência numérica, mas um segredo bem guardado da natureza.
Prepare-se para explorar a sequência que está por trás da aparência deslumbrante das coisas que nos cercam.
É hora de desvendar o mistério da sequência de Fibonacci, e, à medida que mergulhamos nessa jornada matemática, você se verá intrigado, inspirado e cativado, sem dúvida, a continuar sua leitura para descobrir tudo a respeito.
O que é a sequência de Fibonacci
A sequência de Fibonacci é um dos fenômenos matemáticos mais cativantes e onipresentes na natureza e na matemática.
Ela recebe seu nome do matemático italiano Leonardo de Pisa, mais conhecido como Fibonacci, que a introduziu no mundo ocidental em seu livro Liber Abaci no início do século XIII.
A sequência começa de forma simples, com dois termos iniciais: $0$ e $1$. A partir desses termos, cada termo subsequente é gerado pela soma dos dois termos anteriores.
Ou seja $$F_{n+2}=F_{n+1}+F_n,$$com $F_0=0$ e $F_1=1$.
Com isso, os primeiros termos da sequência de Fibonacci são $$0,1,1,2,3,5,8,13,21,34,\ldots.$$
Cada termo dessa sequência é chamado de número de Fibonacci.
O primeiro fato que destacamos aqui é a relação dos números de Fibonacci com o número de ouro $$\phi=\frac{1+\sqrt{5}}{2}=1,61803398874989484820458683\ldots.$$
De fato, à medida que avançamos na sequência, o quociente entre um número de Fibonacci e o seu antecessor se aproximam de $\phi$:
$$\frac{34}{21}=1,619047619047\ldots.$$
$$\frac{55}{34}=1,617647058823\ldots$$ e
$$\frac{4181}{2584}=1,618034055727\ldots.$$
Sequência de Fibonacci: História e origens

Para entender plenamente a importância dessa sequência, é essencial explorar as suas origens e seu papel na evolução da matemática e da ciência ao longo dos séculos.
A história da sequência de Fibonacci começa com o matemático italiano Leonardo de Pisa, mais conhecido como Fibonacci.
Ele nasceu por volta de 1170 e cresceu em Pisa, Itália.
Fibonacci é lembrado principalmente por seu trabalho revolucionário Liber Abaci.
Este livro foi fundamental na introdução de um sistema de numeração indo-arábico na Europa, que substituiu o sistema romano antiquado e ainda é amplamente utilizado hoje.
A obra também introduziu a sequência que leva seu nome.
Dentro do “Liber Abaci”, Fibonacci descreveu a sequência que agora leva seu nome como uma solução para um problema envolvendo o crescimento de uma população de coelhos.
A sequência começa com $0$ e $1$, e os termos subsequentes são gerados pela soma dos dois anteriores $(0, 1, 1, 2, 3, 5, 8, 13, \ldots)$.
No contexto do problema dos coelhos, cada termo representava o número de coelhos após cada mês.
Essa ideia simples, embora originalmente destinada a fins biológicos, tornou-se um dos pilares mais importantes da matemática.
Embora Fibonacci tenha popularizado a sequência em seu livro, a ideia subjacente remonta muito antes de sua época.
O matemático indiano Pingala, em seu trabalho “Chandaḥśāstra” datado de aproximadamente 450 a.C., mencionou uma sequência de números semelhante em conexão com métrica poética.
Essa sequência, na verdade, prenunciava a sequência de Fibonacci, embora não tenha sido reconhecida como tal na época.
A sequência de Fibonacci não se limita apenas à história; ela tem uma relevância contínua na matemática e em várias outras disciplinas.
A relação com o número de ouro a torna uma ferramenta valiosa na arte e na arquitetura.
Propriedades da sequência de Fibonacci
Nesta seção, vamos explorar essas propriedades e entender por que a sequência de Fibonacci é um dos tópicos mais intrigantes da matemática.
Propriedade de Lamé
A primeira propriedade que trazemos aqui é devida ao matemático francês Gabriel Lamé (1795-1870).
Ele mostrou que na sequência de Fibonacci deve haver pelo menos quatro números e no máximo cinco números com o mesmo número de dígitos.
Em outras palavras, nunca haveria apenas três números de Fibonacci com um certo número de dígitos, nem haveria até seis números de Fibonacci com um determinado número de dígitos.
Soma de 10 números de Fibonacci consecutivos
Uma outra propriedade envolvendo os números de Fibonacci é que a soma de $10$ números de Fibonacci consecutivos é divisível por $11$.
Vejamos um exemplo:
$$1+1+2+3+5+8+13+21+34+55=143$$
que é $11\cdot 13$.
Para ver isso, sejam $F_k, F_{k+1},\ldots, F_{k+9}$, $10$ números de Fibonacci consecutivos.
$$F_{k+2}=F_{k}+F_{k+1},$$
$$F_{k+3}=F_{k+1}+F_{k+2}=F_k+2F_{k+1},$$
$$F_{k+4}=F_{k+2}+F_{k+3}=2F_k+3F_{k+1},$$
$$F_{k+5}=F_{k+3}+F_{k+4}=3F_k+5F_{k+1},$$
$$F_{k+6}=F_{k+4}+F_{k+5}=5F_k+8F_{k+1},$$
$$F_{k+7}=F_{k+5}+F_{k+6}=8F_k+13F_{k+1},$$
$$F_{k+8}=F_{k+6}+F_{k+7}=13F_k+21F_{k+1}$$
e $$F_{k+9}=F_{k+7}+F_{k+8}=21F_k+34F_{k+1}.$$
Portanto, $$\sum_{i=0}^9F_{k+i}=55F_k+88F_{k+1}=11\cdot(5F_k+8F_{k+1}).$$
A soma de $n$ primeiros números de Fibonacci
A terceira propriedade relacionada à sequência de Fibonacci que apresentamos aqui envolve a soma dos $n$ primeiros números de Fibonacci.
Para isso, lembremos da relação $F_{n+2}=F_{n+1}+F_n,$ com $n\geq 1$.
Segue daí que $$F_n=F_{n+2}-F_{n+1}.$$
Com isso, temos
\begin{eqnarray*}
F_1&=&F_3-F_2\\
F_2&=&F_4-F_3\\
F_3&=&F_5-F_4\\
F_4&=&F_6-F_5\\
&&\quad\vdots\\
F_{n-1}&=&F_{n+1}-F_n\\
F_n&=&F_{n+2}-F_{n+1}
\end{eqnarray*}
Agora somamos essas equações.
Observe que ao somarmos essas equações, eliminamos vários termos no lado direito (porque sua soma é zero).
Assim, $$\sum_{i=1}^nF_i=F_{n+2}-F_2=F_{n+2}-1.$$
Fórmula de Binet
A fórmula de Binet é uma expressão matemática que permite calcular o valor de qualquer termo da sequência de Fibonacci sem a necessidade de realizar cálculos repetitivos ou recursivos.
A fórmula, devida ao matemático francês Jacques-Philippe-Marie Binet (1786-1856), é a seguinte:
$$F_n=\frac{1}{\sqrt{5}}\left[\left(\frac{1+\sqrt{5}}{2}\right)^n-\left(\frac{1-\sqrt{5}}{2}\right)^n\right]$$
A sequência de Fibonacci ainda é um tema atual de pesquisa.
De fato, a Fibonacci Quarterly é uma revista científica sobre temas matemáticos relacionados aos números de Fibonacci publicada quatro vezes por ano.
Aplicações da sequência de Fibonacci
Na natureza
A presença da sequência de Fibonacci na natureza é uma das manifestações mais impressionantes de sua relevância.
Ela é encontrada em inúmeros fenômenos naturais, desde conchas espirais até a disposição das folhas em plantas.
Considere, por exemplo, um abacaxi.
Nele podem ser vistas brácteas hexagonais em fileiras que se estendem em três direções distintas.
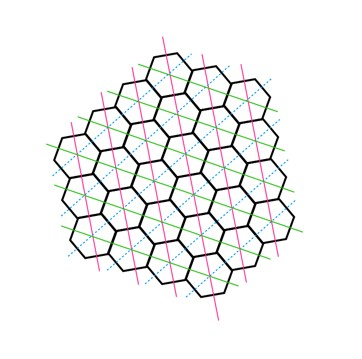
Em 1970, Onderdonk observou que a maioria dos abacaxi tinha fileiras com 8, 13 e 21 brácteas e alguns menores com 5, 8 e 13.
Na arte e arquitetura
A aplicação da sequência de Fibonacci na arte e na arquitetura tem a ver com sua relação com o número de ouro $\phi$.
Durante séculos, arquitetos e artistas identificaram o que eles acreditavam ser o retângulo de formato perfeito. Aquele, no qual, a razão entre o comprimento do lado maior e o do lado menor é igual ao número de ouro.
Por isso, esse retângulo é chamado de retângulo de ouro.
Se você esboçar um retângulo envolvendo a vista frontal do Partenon em Atenas, Grécia, você terá desenhado um retângulo de ouro.

Na famosa pintura de Leonardo da Vinci, Mona Lisa, pode-se desenhar um retângulo em torno do rosto de Mona Lisa e descobrir que se trata de um retângulo de ouro.
Conclusão
A sequência de Fibonacci é verdadeiramente uma das maravilhas da matemática, com raízes históricas profundas e uma série de propriedades cativantes.
Neste artigo, exploramos os aspectos fundamentais desta sequência e sua relevância em vários campos.
Como matemáticos e entusiastas da matemática, lembramos da importância de entender e apreciar as maravilhas que a matemática pode nos oferecer.
A sequência de Fibonacci é um exemplo brilhante disso, um lembrete de que a matemática é uma linguagem universal que nos conecta a todos.
0 Comentários