A resolução de problemas matemáticos desempenha um papel fundamental em nosso cotidiano, transcende os limites das salas de aula e permeia inúmeras situações da vida real.
Desde calcular despesas domésticas até enfrentar desafios complexos várias áreas da matemática, a habilidade de resolver problemas matemáticos é uma ferramenta valiosa e indispensável.

No entanto, é comum que muitos estudantes enfrentem obstáculos significativos ao lidar com questões matemáticas.
A abordagem abstrata e a natureza desafiadora desses problemas frequentemente geram frustração e insegurança.
A falta de confiança na compreensão dos conceitos fundamentais ou na aplicação de fórmulas e métodos adequados pode tornar a matemática um território intimidante.
Nesse artigo, nosso objetivo é fornecer estratégias e métodos eficazes que não apenas simplifiquem a resolução de problemas matemáticos, mas também ajudem a desenvolver uma abordagem sistemática e confiante diante de desafios numéricos.
Ao longo das próximas seções, exploraremos uma gama diversificada de estratégias aplicáveis a problemas de diversas áreas da matemática.
Nós queremos oferecer ferramentas que possam se adaptar a uma ampla variedade de contextos, abrangendo desde equações algébricas até problemas geométricos.
Portanto, leia este artigo com a mente aberta para explorar dicas práticas e exemplos elucidativos que o conduzirão pelo universo desafiador, mas gratificante, da resolução de problemas matemáticos.
Compreendendo a Natureza dos Problemas Matemáticos

A vastidão dos problemas matemáticos abarca um espectro amplo, variando desde questões elementares até desafios de alta complexidade que exigem uma compreensão profunda dos conceitos envolvidos.
Dentro desse panorama diversificado, os problemas matemáticos podem ser classificados em várias categorias, cada uma com suas características distintas e métodos específicos de abordagem.
Desde problemas aritméticos simples, que envolvem operações básicas como adição, subtração, multiplicação e divisão, até problemas de cálculo avançado, que demandam técnicas mais elaboradas, como integração e diferenciação, a matemática abrange uma ampla gama de desafios.
Entretanto, independente do nível de dificuldade, todos os problemas matemáticos compartilham certos elementos-chave que são cruciais para sua resolução.
A habilidade de identificar informações relevantes dentro do enunciado do problema é fundamental.
Muitas vezes, a pergunta apresentada pode conter informações aparentemente desnecessárias, exigindo do solucionador a capacidade de discernir o que é essencial para resolver o problema.
Além disso, compreender completamente a natureza da pergunta é um ponto crucial.
Por vezes, problemas matemáticos são formulados de maneira a requerer uma interpretação cuidadosa.
A capacidade de traduzir a linguagem matemática para uma representação compreensível é tão vital quanto a habilidade de aplicar fórmulas ou algoritmos.
Outro elemento-chave é a habilidade de discernir as operações e métodos necessários para resolver o problema.
Isso implica não apenas conhecer uma variedade de técnicas matemáticas, mas também saber quando e como aplicá-las de forma eficaz.
Por exemplo, em problemas que envolvem geometria, é necessário não apenas compreender as propriedades das figuras envolvidas, mas também escolher o teorema ou método apropriado para alcançar a solução.
Ao dominar esses elementos fundamentais, os desafios apresentados pela matemática se tornam mais acessíveis, permitindo uma abordagem mais estruturada e eficaz na resolução de problemas matemáticos.
Estratégias Gerais para Resolver Problemas Matemáticos
A resolução de problemas matemáticos muitas vezes é aprimorada pela adoção de estratégias gerais que transcendem a aplicação direta de fórmulas e teoremas.
Estas estratégias oferecem um guia valioso para enfrentar problemas de forma mais eficaz e estruturada.
Modelagem Matemática
A modelagem matemática representa uma abordagem poderosa para a resolução de problemas.
Essa técnica consiste em traduzir situações do mundo físico ou abstrato em modelos matemáticos.
Ao identificar variáveis-chave, estabelecer relações entre elas e formular equações ou sistemas, os problemas complexos são simplificados, permitindo sua resolução por métodos matemáticos convencionais.
Abordagem Sistemática
A decomposição de problemas complexos em etapas menores é uma estratégia-chave para simplificar a resolução de problemas.
Ao dividir um problema em partes menores e mais gerenciáveis, torna-se mais fácil compreender e abordar cada componente separadamente.
Isso não apenas facilita o processo de resolução, mas também reduz a possibilidade de erros ao lidar com uma quantidade menor de informações de cada vez.
Uso de Recursos
A disponibilidade de recursos educacionais é um aliado importante na resolução de problemas matemáticos.
Livros didáticos, plataformas online, softwares especializados e vídeos educativos oferecem uma riqueza de informações e exemplos que podem auxiliar na compreensão de conceitos complexos.
Livros didáticos específicos para diferentes áreas da matemática podem oferecer explicações passo a passo e exercícios variados para praticar.
Plataformas online e softwares especializados fornecem interatividade e ferramentas úteis para visualização de conceitos, simulação de problemas e prática adicional.
Além disso, vídeos educativos e tutoriais online podem oferecer uma abordagem complementar, explicando conceitos de forma dinâmica e visualmente atrativa.
A combinação inteligente e a utilização adequada desses recursos podem fornecer suporte valioso, ajudando os estudantes a aprimorarem suas habilidades na resolução de problemas matemáticos e a desenvolverem uma compreensão mais profunda dos conceitos apresentados.

Estratégias Específicas para Diferentes Tipos de Problemas

Antes de resolver qualquer problema, leia-o por completo para descobrir que tipo de problema é e do que se trata.
Preste atenção no que se pede no fim da questão, pois é aí que você vai descobrir o que tem que achar.
Veja a seguir alguns passos que você terá que seguir para resolver problemas de várias áreas da matemática.
Problemas de Álgebra
A grande maioria dos problemas (ou situações problemas) de álgebra são resolvidas através de equações, sistemas de equações ou inequações.
Esses problemas envolvem relações entre números, cálculo de idades, cinemática, finanças, etc.
Seguindo a seção acima de Modelagem Matemática, escolha letras para indicar as quantidades procuradas no problemas.
O passo seguinte é traduzir o problema para a linguagem matemática. Aqui, você deve representar, usando símbolos matemáticos, relações entre a quantidade desconhecida e as quantidades conhecidas do problema.
Você deverá chegar em alguma equação, sistema de equações ou uma inequação.
Em seguida, use operações matemáticas conhecidas para resolver as equações.
Por fim, verifique se a resposta encontrada resolve de fato o problema.
Exemplo 1: Resolvendo problemas usando equações
Divida $90$ em duas partes de modo que $7$ vezes a parte menor seja $6$ a mais que $5$ vezes a parte maior.
Solução.
Seja $x$ a parte menor.
Assim, a parte maior é $90-x$.
O trecho do problema “$7$ vezes a parte menor” é representado por $7x$.
A palavra “seja” será substituído pelo símbolo $=$.
E representamos “$6$ a mais que $5$ vezes a parte maior” por $5(90-x)+6$.
Portanto, a equação obtida é $$7x=5(90-x)+6.$$
Resolvendo-a, temos
\begin{eqnarray*}
7x=450-5x+6 &\Rightarrow& 12x=456\\
&\Rightarrow& x=\frac{456}{12}=38.
\end{eqnarray*}
Assim, a parte menor é $38$ e a parte maior é $90-38=52$.
Por fim, observe que $7\cdot 38=266$ e $5\cdot 52+6=260+6=266$, ou seja, $$7\cdot 38=5(90-38)+6,$$ o que mostra que a solução encontrada da equação está, de fato, correta.
Exemplo 2: Resolvendo um problema usando sistema de equações
Em uma livraria, João vende canetas por R\$ 1,20 cada e cadernos por R\$ 3,50 cada. Ele ganhou um total de R\$ 91,70 vendendo um total de 40 canetas e cadernos juntos. Determine o número de canetas e o número de cadernos vendidos.
Solução.
Sejam $x$ o número de canetas e $y$ o número de cadernos.
Como João vende uma caneta por R\$ 1,20 cada e um caderno por R\$3,50 e ele ganhou R\$ 91,70 ao vender 40 itens (canetas e cadernos), temos o seguinte sistema de equações:
$$\left\{\begin{array}{l}
1,20x+3,50y=91,70\\
x+y=40.
\end{array}\right.$$
Da segunda equação, segue que $y=40-x$. Substituindo na primeira equação, obtemos $$1,20x+3,50(40-x)=91,70,$$ o que implica $$-2,30x=91,70-140=-48,30,$$ ou seja, $$x=\frac{-48,30}{-2,30}=21.$$
De $y=40-x$, obtemos $y=19$.
Como $21+19=40$ e $1,20\cdot 21+3,50\cdot 19=91,70$, a solução encontrada está correta.
Assim, João vendeu $21$ canetas e $19$ cadernos.
Exemplo 3: Resolvendo um problema usando inequações
Se você encontrar em um problema expressões como
- no máximo,
- maior que,
- não menos que,
- no mínimo,
- pelo menos,
- menor que,
- não mais que
ou qualquer outra expressão com o significado semelhante, então há uma boa chance que esse problema deve ser resolvido usando inequações.
Vejamos um exemplo.
Ana tem R\$ 800 em sua conta no início das férias de verão. Ela deseja ter pelo menos R\$ 300 ao final das férias. Ana retira R\$ 40 por semana para alimentação, roupas e ingressos de cinema. Quantas semanas Ana pode retirar dinheiro de sua conta?
Solução.
Seja $x$ o número de semanas em que Ana retira dinheiro de sua conta.
A quantidade total retirada após $x$ semanas será $40x$. A quantidade final de dinheiro que ela terá é dada por $800-40x$.
Queremos que essa quantia seja maior ou igual a R$ 300. Então, a inequação fica assim:
$$800-40x\geq 300.$$
Agora, podemos resolver essa inequação para encontrar o valor de $x$:
\begin{eqnarray*}
800-40x&\geq& 300\\
40x&\leq& 800-300\\
40x&\leq& 500\\
x&\leq& \frac{500}{40}\\
x&\leq& 12,5
\end{eqnarray*}
Portanto, Ana pode retirar dinheiro de sua conta por até 12 semanas para garantir que ela tenha pelo menos R\$ 300 ao final das férias.
Geometria e Trigonometria
Problemas geométricos frequentemente requerem uma compreensão sólida das propriedades das formas e ângulos.
Problemas de Geometria e Trigonometria, na maioria das vezes, requerem um entendimento de relações básicas entre retas, ângulos e polígonos.
Além disso, é crucial familiarizar-se com teoremas, como o teorema de Pitágoras, teorema de Tales, e regras de congruência e semelhança de triângulos.
Na trigonometria, o uso das razões trigonométricas (seno, cosseno e tangente) é crucial.
Resolver problemas que envolvem ângulos, triângulos e identificação de padrões geométricos é facilitado com o entendimento dessas relações trigonométricas.
Uma estratégia bastante utilizada nesse contexto é desenhar figuras e diagramas.
Exemplo 1
Um mastro de bandeira está verticalmente posicionado em um terreno escolar. Duas cordas de comprimento igual estão presas do topo do mastro para dois pontos fixos no chão, formando um ângulo de $40$º entre si. Quais são as medidas dos ângulos formados pelas cordas e o chão?
Solução.
Como as cordas têm o mesmo comprimento, obtemos um triângulo isósceles.
Em um triângulo isósceles, os ângulos opostos aos lados congruentes são congruentes. Assim, vamos chamar de $x$ a medida dos ângulos formados pelas cordas e o chão.
A figura abaixo ilustra bem a nossa situação.
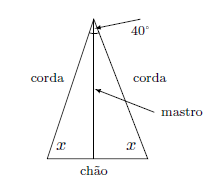
Agora, para encontrar o valor de $x$, usaremos o fato conhecido que a soma das medidas dos ângulos de um triângulo é $180$°.
Temos
\begin{eqnarray*}
x+x+40&=&180\\
2x&=&140\\
x&=&70
\end{eqnarray*}
Logo, cada corda forma um ângulo de $70$° com o chão.
Exemplo 2
A diagonal de um retângulo mede $10$ cm e forma um ângulo de $60$° com o lado mais curto. Qual é o perímetro do retângulo?
Solução. Façamos uma figura para visualizamos a situação.
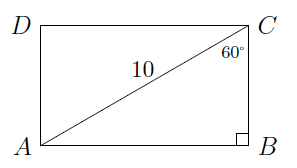
Sejam $x=\overline{AB}$ e $y=\overline{BC}$. Temos $$\mbox{sen}\; 60°=\frac{x}{10}\Rightarrow \frac{\sqrt{3}}{2}=\frac{x}{10},$$ o que implica $x=5\sqrt{3}$.
Além disso, $\cos 60°=\dfrac{y}{10}$, o que implica $\dfrac{1}{2}=\dfrac{y}{10}$, ou seja, $$y=5.$$
Portanto, o perímetro do retângulo é $$2\cdot 5\sqrt{3}+2\cdot 5=10\sqrt{3}+10.$$

Conclusão
Desenvolver habilidades nessas áreas envolve prática constante, resolução de problemas variados e a aplicação de conceitos fundamentais em diferentes contextos.
Essas estratégias específicas para diferentes ramos da matemática fornecem um ponto de partida sólido para lidar com problemas específicos de cada área.
No entanto, é importante notar que a prática contínua e a exploração de problemas diversificados são essenciais para aprimorar essas habilidades e tornar-se mais proficientes na resolução de problemas matemáticos complexos em diversas áreas.




0 Comentários