Você sabia que é possível calcular o número de diagonais de um polígono de forma simples e direta, independentemente do formato da figura?
Embora o cálculo do número de diagonais pareça simples, é importante entender a lógica por trás da fórmula e como ela se aplica a diferentes tipos de polígonos.
Neste artigo, vamos desvendar a fórmula para calcular o número de diagonais de um polígono, aplicando-a tanto a polígonos convexos quanto côncavos, e esclarecer como podemos fazer esse cálculo de maneira prática.
Polígonos
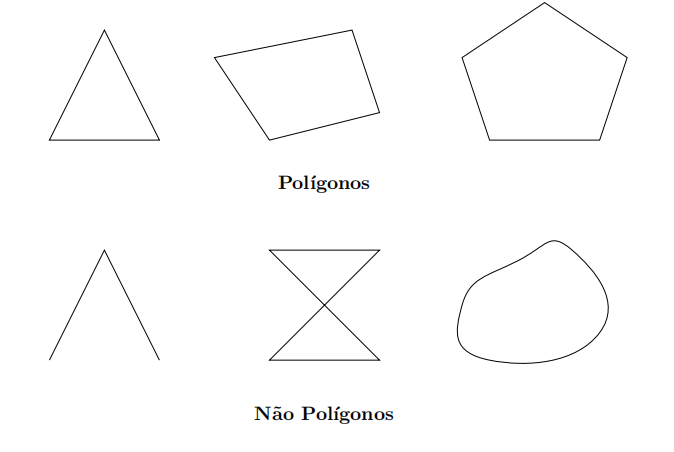
Um polígono é uma figura geométrica plana fechada formada por segmentos de reta que se conectam nas suas extremidades.
Desse modo, a união desses segmentos formam borda contínua que delimita uma região no plano.
Cada segmento de reta é chamado de lado e cada ponto de encontro dos segmentos é chamado de vértice.
Em outras palavras, para uma figura geométrica plana ser um polígono, ela deve atender a alguns critérios:
- não possuir lados curvos;
- não possuir lados que se cruzam e
- possuir pelo menos três lados.
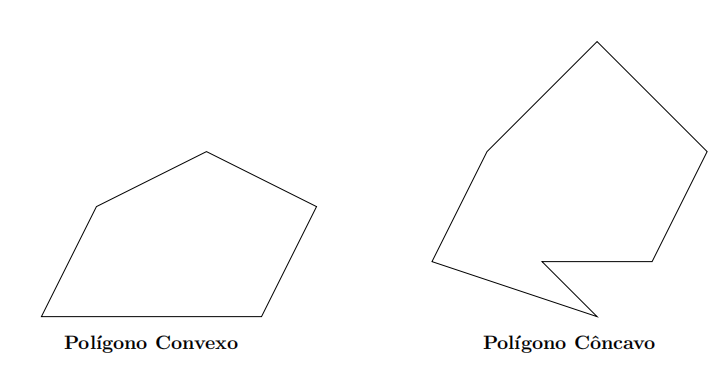
Podemos classificar os polígonos em
- convexos: todos os ângulos internos têm medidas menores do que 180° ou
- côncavos: possuem pelo menos um ângulo interno cuja medida é maior do que 180°.
O que é diagonal de um polígono?
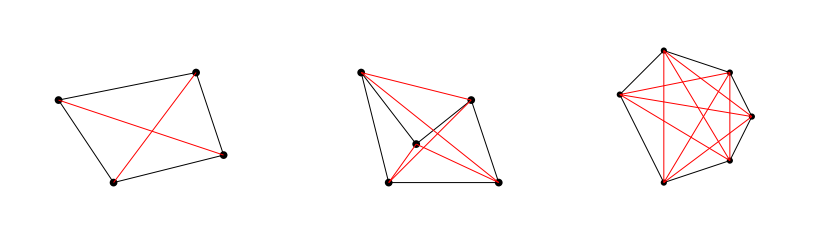
Em um polígono, uma diagonal é um segmento de reta que liga dois vértices não adjacentes.
Ou seja, uma diagonal sempre parte de um vértice e vai até outro, sem ser um dos lados do polígono.
Por exemplo,
- um quadrilátero tem duas diagonais;
- um pentágono tem cinco diagonais;
- um hexágono tem nove diagonais, etc.
Agora que entendemos o que são polígonos e suas diagonais, vamos ver a fórmula que nos permite calcular o número de diagonais de qualquer polígono a partir do número de seus lados.
A fórmula para calcular o número de diagonais de um polígono
Seja $n$ o número de lados (ou vértices) de um polígono. A fórmula para calcular o número de diagonais é: \[d=\frac{n(n-3)}{2}.\]
Entendendo a fórmula
Cada vértice de um polígono pode ser ligado a outro vértice por um segmento de reta.
Porém, nem toda ligação entre vértices forma uma diagonal. Um vértice não pode ser ligado a ele mesmo por um segmento de reta, e, além disso, ao ligarmos um vértice a um de seus dois vizinhos imediatos, formamos apenas os lados do polígono, não diagonais.
Assim, de cada vértice, podemos traçar $n-3$ diagonais:
- Não podemos ligá-lo a ele mesmo (1 vértice a menos).
- Não podemos ligá-lo aos seus dois vizinhos (2 vértices a menos).
Portanto, em um polígono com $n$ vértices, inicialmente contaríamos $n(n-3)$ ligações. Como cada diagonal é contada duas vezes (uma de cada extremidade), dividimos por 2 para obter o número correto de diagonais:
$$d = \frac{n(n-3)}{2}.$$
Exemplos
- Triângulo \(n = 3\): \[
d = \frac{3(3-3)}{2} = \frac{3(0)}{2} = 0
\] Um triângulo não possui diagonais. - Quadrilátero \(n = 4\): \[
d = \frac{4(4-3)}{2} = \frac{4(1)}{2} = 2
\] Um quadrilátero possui 2 diagonais. - Pentágono \(n = 5\): \[
d = \frac{5(5-3)}{2} = \frac{5(2)}{2} = 5
\] Um pentágono possui 5 diagonais. - Decágono \(n = 10\): \[
d = \frac{10(10-3)}{2} = \frac{10 \times 7}{2} = \frac{70}{2} = 35
\] Portanto, um decágono tem 35 diagonais!
Observação sobre Polígonos Côncavos
Vale destacar que a fórmula para o número de diagonais, \(d = \frac{n(n-3)}{2}\), também é válida para polígonos côncavos.
Isso ocorre porque a fórmula depende apenas do número de vértices \( n \), e não da forma geométrica específica do polígono.
Mesmo que um polígono tenha um “ângulo com medida maior que 180º” (como nos polígonos côncavos), o número de diagonais permanece o mesmo.
A única diferença é que algumas dessas diagonais podem “passar por fora” do polígono, cruzando uma área externa da figura, mas ainda assim são consideradas diagonais, pois conectam vértices não adjacentes.
Conclusão
Em resumo, a fórmula \( d = \frac{n(n-3)}{2} \) permite calcular o número de diagonais de qualquer polígono, seja ele convexo ou côncavo.
Embora em polígonos côncavos algumas diagonais possam passar “por fora”, todas são contabilizadas de acordo com a fórmula.
Agora que você conhece a fórmula, pode aplicá-la a diferentes polígonos e explorar suas propriedades de forma mais profunda.
Gostou do artigo? Experimente calcular as diagonais de outros polígonos e compartilhe seus resultados nos comentários abaixo! Se tiver dúvidas ou quiser aprender mais sobre geometria, fique à vontade para explorar outros artigos no blog.



0 Comentários