Você sabe o que é mínimo múltiplo comum (MMC) de dois ou mais números e como calculá-lo?
Se você está aqui para relembrar como calcular, como resolver problemas e por que estudar esse assunto, você está no lugar certo.

Aqui você vai ver os pré-requisitos básicos para entender melhor esse conceito. Além disso, você irá conhecer algumas propriedades do MMC justificadas de forma detalhada.
Por fim, você verá problemas típicos de MMC e como resolvê-los.
Então vamos lá!
Vamos começar vendo o que é um múltiplo de um número.
O que é um múltiplo (inteiro) de um número?
Seja $a$ um número inteiro. Um múltiplo inteiro de $a$ é um número da forma $$a\times d.$$
Por exemplo, os múltiplos de 2 são $0=2\times 0$, $2=2\times 1$, $4=2\times 2$ e assim por diante.
Os múltiplos inteiros de um elemento $a$ têm as seguintes propriedades.
1) 0 é um múltiplo de $a$: de fato temos que $$0=0\times a.$$
2) Se $m$ é múltiplo de $a$, então $-m$ também é: se $m$ é múltiplo de $a$, existe $d\in\mathbb{Z}$ tal que $$m=a\times d.$$ Daí, $$-m=-(a\times d)=a\times(-d),$$ o que implica que $-m$ é um múltiplo de $a$.
3) Um múltiplo de um múltiplo de $a$ é também um múltiplo de $a$: Sejam $m$ um múltiplo de $a$ e $M$ um múltiplo de $m$. Temos que $$M=m\times d=(a\times d’)\times d=a\times (d’\times d).$$ Assim, $M$ é um múltiplo de $a$.
4) Se $m$ e $m’$ são múltiplos de $a$, então $r\times m+s\times m’$ é também um múltiplo de $a$: sejam $d, d’$ os inteiros tais que $m=a\times d$ e $m’=a\times d’$. Portanto,
\begin{eqnarray*} r\times m+s\times m’&=&r\times(a\times d)+s\times(a\times d’)\\&=&a\times(r\times d+s\times d’). \end{eqnarray*}
Logo, $r\times m+s\times m’$ é também um múltiplo de $a$.
5) Se $m+m’$ ou $m-m’$ são múltiplos de $a$ e $m$ é múltiplo de $a$, então $m’$ é um múltiplo de $a$: suponhamos que $m+m’$ e $m$ sejam múltiplos de $a$. Assim existem $D, d\in\mathbb{Z}$ tais que $$m+m’=a\times D$$ e $$m=a\times d.$$ Assim, $$m’=(m+m’)-m=a\times D-a\times d=a\times(D-d),$$ o que mostra que $m’$ é um múltiplo de $a$.
Por que estudar MMC?
Se você está aqui é porque quer saber mais sobre Mínimo Múltiplo Comum. E uma das perguntas que pode surgir na sua cabeça é porque você tem que estudar esse assunto.
Sendo assim, eu vou te dar três razões pelas quais você deve estudar esse tema básico da matemática.
Operações com frações
Quando se está trabalhando com adição e subtração de frações você pode precisar encontrar o mínimo múltiplo comum dos denominadores.
Por exemplo, vamos calcular $$\frac{3}{4}+\frac{5}{6}.$$
O MMC de 4 e 6 é 12. Assim, $$\frac{3}{4}+\frac{5}{6}=\frac{9+10}{12}=\frac{19}{12}.$$
Comparação de frações
Você sabe qual das frações $\dfrac{5}{9}$ e $\dfrac{7}{12}$ é a maior?
Para saber qual delas é a maior, encontramos o MMC dos denominadores, escrevemos as frações equivalentes e a as comparamos.
Assim, já que o MMC de 9 e 12 é 36, as frações equivalentes que iremos tomar são $\dfrac{20}{36}$ e $\dfrac{21}{36}$, respectivamente.
Como $$\frac{20}{36}<\frac{21}{36},$$ segue que $$\frac{5}{9}<\frac{7}{12}.$$
Situações-problema
Sem sombra de dúvidas, essa é uma das principais razões para estudar mínimo múltiplo comum.
Os problemas matemáticos sobre MMC estão presentes em várias provas de concursos públicos, por exemplo.
Além de você precisar saber como calcular o MMC de dois ou mais números, você precisa saber como interpretar um problema matemático.
Vejamos um exemplo a seguir.
“Três amigos passeiam de bicicleta, na mesma direção, em torno de uma pista circular rápida. Para dar uma volta completa um deles demora 15 segundos, outro demora 18 segundos e o terceiro demora 21 segundos.
Eles partem juntos e combinam interromper o passeio quando os três se encontrarem pela primeira vez no ponto de partida. Depois de quanto tempo isso irá acontecer?”
Uma vez que eles vão dar voltas completas, o tempo gasto será múltiplo de 15 segundos, por causa do primeiro amigo. Também será múltiplo de 18, por causa do segundo e múltiplo de 21 por causa do terceiro.
Assim, estamos procurando por um múltiplo comum de 15, 18 e 21.
Além disso, queremos saber a primeira vez que que eles irão se encontrar no ponto de partida, ou seja, queremos o mínimo múltiplo comum desses números.
Mas adiante, quando vermos alguns métodos para calcular MMC, iremos voltar para esse problema para terminá-lo.
O que é o MMC de dois números?
Sejam $a$ e $b$ dois números inteiros. Um inteiro $m$ que é um múltiplo de $a$ e de $b$ é chamado de múltiplo comum.
Considere os conjuntos dos múltiplos de $a$ e $b$:
$$a\mathbb{Z}=\{a\times d; d\in\mathbb{Z}\}$$ e $$b\mathbb{Z}=\{b\times d; d\in\mathbb{Z}\}$$
Assim, o conjunto $$a\mathbb{Z}\cap b\mathbb{Z}$$ é o conjunto dos múltiplos comuns de $a$ e de $b$.
Suponha que $a$ e $b$ são ambos não nulos. O mínimo múltiplo comum de $a$ e $b$, denotado por $\textrm{mmc}(a,b)$ é o menor múltiplo comum positivo.
Ou seja, é o menor elemento positivo do conjunto $$a\mathbb{Z}\cap b\mathbb{Z}.$$
Se um dos números é nulo e o outro é um inteiro qualquer, o único múltiplo comum é o 0 e esse será o mínimo múltiplo comum.
Se você preferir, você pode voltar a sua atenção somente para os números naturais (inteiros positivos).
Nesse caso, o mínimo múltiplo comum de dois naturais $a$ e $b$ é simplesmente o menor múltiplo comum não nulo de $a$ e $b$.
Por exemplo, consideremos os múltiplos de 12 e de 15: $$12\mathbb{Z}=\{0,\pm12, \pm24, \pm36, \pm48, \pm60, \pm72,\ldots\}$$ e $$15\mathbb{Z}=\{0,\pm15, \pm30, \pm45, \pm60, \pm75,\ldots\}.$$
Daí, temos $$12\mathbb{Z}\cap15\mathbb{Z}=\{0,\pm60,\pm 120,\ldots\}.$$
Como o menor elemento positivo em $12\mathbb{Z}\cap 15\mathbb{Z}$ é 60, segue que $$\textrm{mmc}(12,15)=60.$$
Propriedades do MMC
Vejamos agora algumas propriedades do MMC.
Propriedade 1
Sejam $a$ e $b$ números inteiros. Um múltiplo de $\textrm{mmc}(a,b)$ é um múltiplo comum de $a$ e $b$.
De fato, isso segue da 3ª propriedade dos múltiplos que vimos acima.
Propriedade 2
Essa propriedade é a recíproca da afirmação anterior e é mais difícil de demonstrar.
A propriedade é a seguinte: todo múltiplo comum de dois inteiros $a$ e $b$ é múltiplo de $\textrm{mmc}(a, b)$.
Para demonstrar esse fato, começaremos chamando o $\textrm{mmc}(a,b)$ de $m$.
Em seguida, considere um múltiplo comum qualquer $m’$ de $a$ e $b$.
Se $m’=0$, está feito, pois 0 é múltiplo de qualquer inteiro, inclusive de $m$.
Assim, vamos supor que $m’\neq 0$. Isso implica que $a$ e $b$ são ambos não nulos e, por isso, $m>0$.
Pelo algoritmo da divisão, podemos escrever $$m’=mq+r,\;\textrm{com}\; 0\leq r<m.$$
Já que $r=m’-mq$ e $m’, mq$ são múltiplos comuns de $a$ e $b$, segue da propriedade 4 dos múltiplos que $r$ é um múltiplo comum de $a$ e $b$.
Assim, como $r<m$ e $m=\textrm{mmc}(a,b)$, concluímos que $r=0$.
Portanto, $m’=mq$, o que mostra que $m’$ é um múltiplo de $m$, como queríamos.
Segue das propriedades acima que $$a\mathbb{Z}\cap b\mathbb{Z}=\textrm{mmc}(a,b)\mathbb{Z}.$$
Propriedade 3
Essa propriedade vai mostrar como calculamos o mmc de três inteiros.
Sejam $a, b$ e $c$, não nulos. Então $$\textrm{mmc}(a, b, c)=\textrm{mmc}(\textrm{mmc}(a,b),c).$$
De fato, temos que $\textrm{mmc}(a, b, c)$ é o menor elemento positivo do conjunto $$a\mathbb{Z}\cap b\mathbb{Z}\cap c\mathbb{Z}.$$ Daí, como $$(a\mathbb{Z}\cap b\mathbb{Z})\cap c\mathbb{Z}=\textrm{mmc}(a,b)\mathbb{Z}\cap c\mathbb{Z}$$ e $$\textrm{mmc}(a,b)\mathbb{Z}\cap c\mathbb{Z}=\textrm{mmc}(\textrm{mmc}(a,b),c),$$ concluímos que $$\textrm{mmc}(a,b,c)=\textrm{mmc}(\textrm{mmc}(a,b),c).$$
Assim, para calcular o mmc de três números recai-se no cálculo
de dois mmc de dois números.
Por exemplo, vamos calcular $\textrm{mmc}(4,6,9)$. Usando a propriedade 3, temos $$\textrm{mmc}(4,6,9)=\textrm{mmc}(\textrm{mmc}(4,6),9).$$
Primeiro vamos encontrar $\textrm{mmc}(4,6)$. Temos $$4\mathbb{Z}={0,\pm4,\pm8,\pm12,\pm16,\ldots}$$ e $$6\mathbb{Z}={0,\pm6,\pm12,\pm18,\pm24,\ldots}.$$ Como o menor elemento positivo de $4\mathbb{Z}\cap6\mathbb{Z}$ é 12, segue que $\textrm{mmc}(4,6)=12.$
Assim, $$\textrm{mmc}(4,6,9)=\textrm{mmc}(12,9).$$
Agora, temos $$12\mathbb{Z}={0,\pm12,\pm24,\pm36,\ldots}$$ e $$9\mathbb{Z}={0,\pm9,\pm18,\pm 27,\pm36,\ldots}.$$ Logo, $\textrm{mmc}(12,9)=36$ e, portanto, $$\textrm{mmc}(4,6,9)=36.$$
Propriedade 4
Sejam $a$ e $b$ dois inteiros positivos. Tem-se a seguinte
identidade:
$$\textrm{mmc}(a,b)\times\textrm{mdc}(a,b)=a\times b.$$
Vamos a seguir demonstrar esse fato.
Já que $a$ é um múltiplo de $\textrm{mdc}(a,b)$, $a\times b$ também o é. Assim, existe $m$ inteiro positivo tal que $$a\times b=m\times \textrm{mdc}(a,b).$$
Como $\textrm{mdc}(a,b)$ é um divisor comum de $a$ e $b$, $m$ tem que ser um múltiplo comum de $a$ e $b$. De fato, de $$a=a’\times \textrm{mdc}(a,b)$$ e $$b=b’\times \textrm{mdc}(a,b)$$ temos $$a’\times \textrm{mdc}(a,b)\times b=m\times \textrm{mdc}(a,b)$$ o que implica que $m=a’\times b$ o que mostra que $m$ é um múltiplo de $b$.
Similarmente, mostramos que $m$ é um múltiplo de $a$.
Com isso, segue da propriedade 2, que existe $c$ inteiro positivo tal que $$m=c\times \textrm{mmc}(a,b).$$
Assim,
\begin{eqnarray*}
a\times b&=&(c\times \textrm{mmc}(a,b))\times \textrm{mdc}(a,b)\\&=&\textrm{mmc}(a,b)\times(c\times \textrm{mdc}(a,b))
\end{eqnarray*}
Uma vez que $\textrm{mmc}(a,b)$ é um múltiplo comum de $a$ e $b$, existem $d_1$ e $d_2$ tais que $$\textrm{mmc}(a,b)=a\times d_1\quad\textrm{e}\quad\textrm{mmc}(a,b)=b\times d_2.$$ Com isso, substituindo essas expressões na última igualdade, obtemos $$b=d_1\times (c\times \textrm{mdc}(a,b))$$ e $$a=d_2\times (c\times (\textrm{mdc}(a,b)),$$ o que mostra que $c\times \textrm{mdc}(a,b)$ é um divisor comum de $a$ e $b$. Logo, $$c\times \textrm{mdc}(a,b)\leq\textrm{mdc}(a,b).$$ Por outro lado, temos que $c\geq 1$, o que implica que $$c\times \textrm{mdc}(a,b)\geq \textrm{mdc}(a,b).$$ Assim, $c=1$ e por isso, $$a\times b=\textrm{mmc}(a,b)\times \textrm{mdc}(a,b),$$ como queríamos demonstrar.
Métodos para calcular MMC
Agora vamos ver como calculamos MMC de dois ou mais números na prática.
A seguir veremos 3 métodos para calcular MMC.
Método 1: Por interseção ($U=\mathbb{N}={1,2,3,\ldots}$)
Aqui vamos trabalhar com os números naturais.
Esse método é o mais simples de todos. Entretanto, ele se torna impraticável quando os números são muito grandes.
Ele consiste em encontrar o menor elemento da interseção dos conjuntos de múltiplos de números.
Por exemplo, para calcular $\textrm{mmc}(4,6,9)$ exibimos primeiramente os conjuntos dos múltiplos de 4, 6 e 9: $$M_4=\{4, 8, 12,16,20,24,28,32,36,\ldots\},$$ $$M_6=\{6,12,18,24,30,36,42,48, 54,\ldots\}$$ e $$M_9=\{9,18,27,36,45,54,63,72,81,\ldots\}.$$
Em seguida, obtemos a interseção desses conjuntos $$M_4\cap M_6\cap M_9=\{36,72,\ldots\}.$$
Por fim, determinamos qual o menor elemento desse interseção. Nesse caso o menor valor é 36. Portanto, $$\textrm{mmc}(4,6,9)=36.$$
Método 2: Decomposição em fatores primos
Esse método consiste em decompor em fatores primos dos números que queremos calcular o MMC e tomar aqueles fatores primos com maior expoente e multiplicá-los.
Como exemplo, vamos calcular o MMC de 24 e 30.
As fatorações desses números são $$24=2^3\times 3$$ e $$30=2\times 3\times 5.$$ Para um melhor entendimento, podemos escrever $24=2^3\times 3\times 5^0.$
Agora tomamos os fatores primos com maior expoente: $2^3, 3$ e $5$. Portanto, $$\textrm{mmc}(24,30)=2^3\times 3\times 5=120.$$
Método 3: Processo da decomposição simultânea
Esse método consiste em decompor, simultaneamente, os números dados em fatores primos.
Para fazer isso, trace uma reta vertical, onde ficarão os divisores simultâneos. Abaixo de cada número, colocamos o quociente obtido.
O passo a passo do método é assim:
- Começa-se dividindo por 2, caso hajam números divisíveis por 2 quando não for mais possível dividir por 2,
- passamos ao 3 (caso hajam números divisíveis por 3),
- depois segue-se com 5, 7, 11 e assim por diante, até que todos os quocientes sejam 1.
Vejamos como calcular $\textrm{mmc}(12,15,18)$ usando esse método.
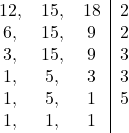
Agora para obter o MMC, basta multiplicar os números que estão à direita da reta.
Portanto, $$\textrm{mmc}(12,15,18)=2^2\times 3^2\times 5=180.$$
Problemas resolvidos sobre MMC
Problema 1
FUNDATEC – 2018 – Prefeitura de Rondinha – RS – Auxiliar Docente
O Mínimo Múltiplo Comum entre os números 36, 48 e 90 é:
a) 960.
b) 720.
c) 540.
d) 360.
e) 120.
Solução
Usando o método da decomposição simultânea temos

Assim, $$\textrm{mmc}(36, 48, 90)=2^4\times 3^2\times 5=720$$ e alternativa correta é a b).
Problema 2
CPCON – 2018 – Prefeitura de Serra Branca – PB – Agente de Saúde
Em um hospital a técnica de enfermagem Raquel trabalha em plantão de três em três dias; a enfermeira chefe, Nanci, de seis em seis dias; e a médica Sandra de oito em oito dias. Sabendo que elas trabalharam juntas no dia 01 de janeiro de 2018, qual a próxima data em que elas irão trabalhar juntas novamente?
a) 25 de janeiro de 2018.
b) 28 de janeiro de 2018.
c) 29 de janeiro de 2018.
d) 02 de fevereiro de 2018
e) 07 de fevereiro de 2018
Solução
Primeiro devemos descobrir depois de quantos dias elas irão trabalhar juntas novamente.
Esse número de dias deve ser um múltiplo comum de 3, 6 e 8. Além disso, estamos interessados na próxima data, assim, queremos determinar $\textrm{mmc}(3,6,8)$.
Já que $3=3$, $6=2\times 3$ e $8=2^3$, usando o método 2, concluímos que $$\textrm{mmc}(3,6,8)=2^3\times 3=24.$$
Portanto, elas irão trabalhar juntas novamente 24 dias depois, ou seja, no dia 25 de janeiro de 2018.
Logo, a alternativa correta é a a).
Problema 3
(PMB)
Um paciente toma duas medicações, uma de 6 em 6 horas e outra de 4 em 4 horas. Ele começou a tomar essa medicação às 6 horas do dia 12/01, tomando os dois remédios ao mesmo tempo. Então, ele voltará a tomar os dois remédios juntos às:
a) 12h.
b) 14h.
c) 18h.
d) 20h.
e) 22h.
Solução
Para descobrir depois de quantas horas ele tomará as duas medicações novamente, basta determinar $\textrm{mmc}(6,4)$.
Vamos fazer esse cálculo, usando o método 1.
Temos $$M_6=\{6, 12, 18,24, 30,\ldots\}$$ e $$M_4=\{4, 8, 12, 16, 20,\ldots\}.$$
Daí, $$M_6\cap M_4=\{12, 24,\ldots\}.$$ Assim, $$\textrm{mmc}(6,4)=12.$$
Como ele tomou a primeira vez às 6h, ele tomará novamente às 18h. Portanto, a alternativa correta é a c).
Problema 4
O MMC de 12, 15, 20 e $k$ é 420. Qual o menor valor de $k$?
Solução
Vamos olhar as fatorações de 12, 15, 20 e 420. Temos $$12=2^2\times 3,$$ $$15=3\times 5,$$ $$20=2^2\times 5$$ e $$420=2^2\times 3\times 5\times 7.$$ Já que $\textrm{mmc}(12, 15, 20, k)=420$ e a fatoração de 420 é feita com as maiores potências de primos dos números 12, 15, 20 e $k$, temos que os fatores 2, 3 e 5 já estão com as potências certas, falta apenas o 7, portanto $k = 7.$
Conclusão
Vimos nesse artigo o que é o mínimo múltiplo comum e as razões pelas quais devemos estudá-lo.
Além disso, conhecemos algumas propriedades interessantes que podem ser bastante úteis para resolver problemas.
Por fim, vimos os três métodos principais para se calcular o MMC, são eles:
- interseção dos conjuntos de múltiplos;
- Decomposição em fatores primos;
- Processo da decomposição simultânea.
Agora é com você, busque calcular o mínimo múltiplo comum usando cada um dos métodos acima para usar o que você achar melhor.
Quer dar um próximo passo para fortalecer sua base matemática? No curso Matemática ZERO 2.0 (link afiliado) serão trabalhados sua mentalidade, seu raciocínio lógico e as bases da Matemática (Matemática Básica) que são fundamentais para o seu desenvolvimento nos estudos.




0 Comentários