Máximo Divisor Comum | O que é e como calcular

Saber como calcular o máximo divisor comum (mdc) e como resolver problemas envolvendo esse conceito é de seu interesse?

Esse tema é um dos assuntos que todo aqueles que você deve saber se quiser dominar a matemática básica desejar dominar a matemática básica deve saber.

De fato, além de saber calcular o mdc entre dois números ou mais, é preciso saber interpretar questões nas quais o conceito aparece.

Concurseiros e vestibulandos também não podem ignorar esse tema fundamental, pois além de ser cobrados em concursos e vestibulares o mdc é uma ferramenta muito útil para entender outros assuntos.

Além disso, a interpretação de questões sobre mdc tem que ser um de seus pontos fortes.

E então, você quer saber porque estudar sobre máximo divisor comum, como calculá-lo, conhecer suas propriedades básicas e como resolver problemas?

Continue lendo esse artigo que vamos discutir sobre esses temas a partir de agora.

Por que estudar sobre máximo divisor comum?

Se você é daqueles que se pergunta “para quê eu devo estudar isso?”, você verá a seguir três razões pelas quais você deve estudar sobre máximo divisor comum.

Frações

A primeira razão pela qual você deve saber o que é o mdc, é por causa do estudo das frações.

Às vezes, é necessário simplificar frações com intuito de facilitar os cálculos.

E para fazer essa simplificação para obter uma fração equivalente irredutível, divide-se o numerador e o denominador pelo seu máximo divisor comum.

Por exemplo, considere a fração $\dfrac{36}{72}$. O máximo divisor comum de 36 e 72 é 36, assim, dividindo o numerador e o denominador por 36, obtemos $$\frac{36}{72}=\frac{1}{2}.$$

Álgebra

Uma outra razão pela qual você deve estudar esse assunto é na álgebra, mais precisamente na fatoração em expressões algébricas.

De fato, para efetuar uma fatoração, é necessário saber qual o máximo divisor comum dos coeficientes.

Por exemplo, podemos escrever a expressão algébrica $36x^2+72x$ como $$36x(x+2x).$$

Situações-problema

As situações-problema ou problemas matemáticos são aquelas questões que vêm com enunciados que precisam ser interpretados e traduzidos para linguagem matemática.

Veja a seguir um exemplo típico de problema típico para ser resolvido usando máximo divisor comum.

Sandra tem dois pedaços de pano. Uma peça tem 72 polegadas de largura e a outra peça tem 90 polegadas de largura. Ela quer cortar os dois pedaços em tiras de largura igual, o mais largo possível. De que largura ela deve cortar as tiras?

Não iremos resolver esse problema agora. Ele só foi dado agora apenas para ilustração.

Quando sabermos como calcular o mdc voltaremos para ele.

O que é divisor de um número?

Antes de saber o que é o máximo divisor comum de dois ou mais números, precisamos saber antes o que é divisor de um número.

Dizemos que um número inteiro $d$ é um divisor ou fator de outro inteiro $a$ , se existe um inteiro $c$ tal que $$a=d\times c.$$

Por exemplo, sabemos que $$45=5\times 9,$$ portanto 5 e 9 são divisores de 45.

Outros divisores de 45 são $$-9,-5,\pm1,\pm3,\pm1,3,15 \;\rm{e}\; \pm45.$$

Daqui em diante trabalharemos apenas com divisores positivos.

Uma palavrinha sobre decomposição em primos.

O que é o Teorema Fundamental da Aritmética

Antes de começar a falar sobre o que é o máximo divisor comum de dois ou mais números, eu preciso falar um pouco sobre decomposição de um inteiro em fatores primos.

Primeiro de tudo, um número primo é um número natural diferente de 1 que possui apenas dois divisores distintos, o 1 e ele próprio.

Os números diferentes de 1 e que não são primos, são chamados de compostos.

Por exemplo, os números 2, 3, 5, 37, 3413 e 7919 são números primos.

Já os números 4, 6, 15 e 100 são exemplos de números compostos.

Bom, agora que sabemos o que são os números primos, você está pronto para conhecer o Teorema Fundamental da Aritmética.

Calma, não precisa se assustar!

Esse teorema diz que podemos escrever qualquer número natural diferente de 1 como um produto de números primos (é a chamada decomposição em números primos).

Além disso, o Teorema Fundamental da Aritmética diz que se colocarmos os fatores em ordem crescente, só há uma única forma de fazer essa decomposição.

A seguir, veja alguns números naturais com sua decomposição em primos.

1) $32=2\times 2\times 2\times 2\times 2=2^5$;

2) $37=37$, já que 37 é um número primo.

3) $100=2^2\times 5^2.$

Método prático para decompor um número natural em fatores primos

Saber como decompor um número natural em fatores primos vai ajudar você a determinar o máximo divisor comum de dois ou mais números como veremos mais adiante.

Pensando nisso, eu vou te mostrar um método prático de fazer essa decomposição.

O método consiste em dividir o número pelo menor primo que ele admita como divisor. Com o quociente resultante da primeira divisão deve-se proceder da mesma maneira até que o quociente seja 1.

Exemplo: Decomponha o número 72 em fatores primos.

Solução: Seguindo o método temos

Portanto, a decomposição de 72 em fatores primos é $$72=2\times 2\times 2\times 3\times 3=2^3\times 3^2.$$

O que é o Máximo Divisor Comum?

Finalmente, vamos ao que interessa!

Voltemos ao problema dos pedaços de pano.

O que temos aqui são duas peças de pano de 72 e 90 polegadas.

Ao pedir para que se corte em tiras de largura igual, estamos procurando por um divisor tanto de 72 quanto de 90, ou seja, um divisor comum.

Além disso, ao pedir que seja o mais largo possível, esse divisor tem que ser o maior de todos. Em outras palavras, queremos o máximo divisor comum de 72 e 90.

Assim, dados dois números $a$ e $b$ não simultaneamente nulos, o maior divisor comum de $a$ e $b$ será chamado de máximo divisor comum de $a$ e $b$ e será denotado por $\textrm{mdc}(a,b)$.

Exemplo: Os divisores de 15 são $1,3,5$ e $15$ e os divisores de 35 são $1,5,7$ e $35$.

Observe que os divisores comuns de 15 e 35 são 1 e 5 e que o maior deles é o 5, por isso, $$\textrm{mdc}(15,35)=5.$$

Essa é uma forma de calcular o mdc de dois números, fazer uma lista dos seus divisores e em seguida procurar o maior divisor comum.

Mas nesse caso, não tivemos trabalho algum, pois ambos os números são pequenos.

Quando um dos números é grande, esse método torna-se impraticável, pois achar todos os divisores de números grandes não é tarefa fácil.

Por isso, precisamos conhecer outros métodos para calcular o mdc de dois números. Vamos ver alguns deles mais adiante.

Mas antes, vamos falar de algumas propriedades do mdc.

Propriedades básicas do máximo divisor comum

Algumas propriedades do máximo divisor comum são

1) $\textrm{mdc}(a,b)=\textrm{mdc}(b,a)$;

2) Todo número que for um divisor de $a$ e $b$ é também um divisor de $\textrm{mdc}(a,b)$;

3) $\textrm{mdc}(a,b)=\textrm{mdc}(-a,b)=\textrm{mdc}(a,-b)=\textrm{mdc}(-a,-b)$;

4) $\textrm{mdc}(a,b)=\textrm{mdc}(a,b-a)$;

5) (Identidade de Bézout) Se $d=\textrm{mdc}(a,b)$, então existem $r,s\in\mathbb{Z}$, tais que $d=ar+bs$.

Como calcular o máximo divisor comum?

Como falei anteriormente, existe vários métodos para calcular o mdc de dois ou mais números. Neste artigo, irei te mostrar 03 maneiras de como fazer esse cálculo.para calcular o máximo divisor comum.

Método 1: Usando a decomposição em primos

Para se determinar o mdc de dois ou mais números, procede-se da seguinte maneira:

Decompõe-se os números em fatores primos;
Em seguida, forma-se o produto entre os fatores comuns usando aqueles com menores expoentes.

Para entender melhor, veja o exemplo a seguir.

Exemplo: Determine o $\textrm{mdc}(24,32,48)$.

As fatorações em primos de 24, 32 e 48 são

\begin{eqnarray*}
24&=&2^3\times 3\\
32&=&2^5\\
48&=&2^4\times 3
\end{eqnarray*}

Observe que o número primo que divide os três números é o 2.

Assim, $\textrm{mdc}(24,32,48)$ será a menor potência de 2, ou seja, $$\textrm{mdc}(24,32,48)=2^3=8.$$

Método 2: Processo prático das fatorações simultâneas.

Agora eu vou te mostrar uma forma mais prática para calcular o mdc usando a decomposição em primos.

Considere novamente o exemplo anterior.

Em seguida, coloque os números em sequência: $$24,32,48.$$ Depois divida todos os números pelo menor primo pelo qual eles são divisíveis, nesse caso é o 2.

Repita o processo para o próximo fator primo comum até que não hajam mais primos em comum.

Por fim, multiplique todos os fatores primos na coluna da direita para obter o mdc. Assim, $$\textrm{mdc}(24,32,48)=2\times2\times 2=8.$$

Método 32: Algoritmo do mdc de Euclides

Agora vamos ver como usar o Algoritmo de Euclides para calcular o máximo divisor comum de dois números.

Mas primeiro, vamos conhecer o Lema de Euclides.

Lema de Euclides

Dados $a$ e $b$, os divisores comuns de $a$ e $b$ são os mesmos são os mesmos que os divisores comuns de $a$ e $b-c\times a$ para todo número inteiro $c$ fixado.

Demonstração: Seja $d$ um divisor comum de $a$ e $b$. Então existem inteiros $a’$ e $b’$ tais que $$a=d\times a’\;\textrm{e}\;b=d\times b’.$$

Daí, temos $$b-c\times a=d\times b’-c \times d\times a’=d\times(b’-c\times a’).$$

Assim, $d$ também é um divisor comum de $a$ e $b-c\times a$.

Por outro lado, suponha agora que $d$ é um divisor comum de $a$ e de $b-c\times a$. Daí, $$a=d\times a’\;\textrm{e}\;b-c\times a=d\times n,$$ para certos inteiros $a’$ e $n$.

Portanto,

\begin{eqnarray*}
b&=&b-c\times a+c\times a\\&=&d\times n+c\times d\times a’\\&=&d\times(n+c\times a),
\end{eqnarray*}

ou seja, $d$ é um divisor comum de $a$ e de $b$ e isso conclui a demonstração.

Assim, como você pode perceber, os divisores comuns de $a$ e $b$ são os mesmos divisores comuns de $a$ e $b-c\times a$. Logo tomando o maior divisor comum em ambos casos, obtemos a fórmula $$\textrm{mdc}(a,b)=\textrm{mdc}(a,b-c\times a).$$

Isso permite ir diminuindo a complexidade do problema para torná-lo mais fácil.

Vamos ver agora como aplicar essa ideia para calcular o mdc de dois números.

Por exemplo, como calcular $\textrm{mdc}(4873, 275)$?

Tome o menor valor para ser o $a$ e o maior para ser o $b$, ou seja, $a=275$ e $b=4873$.

Aplicando o algoritmo da divisão, obtemos $$4873= 275\times 17+198,$$ o que implica que $$4873-275\times 17=198.$$

Assim, do Lema de Euclides segue

\begin{eqnarray*}
\textrm{mdc}(4873, 275)&=&\textrm{mdc}(4873-275\times 17, 275)\\&=&\textrm{mdc}(198, 275)
\end{eqnarray*}

Agora, vamos repetir o argumento com $a_1=198$ e $b_1=275$. Já que $$275=198\times 1+77,$$ temos

\begin{eqnarray*}
\textrm{mdc}(198,275)&=&\textrm{mdc}(198, 275-198\times 1)\\&=&\textrm{mdc}(198, 77)
\end{eqnarray*}

Novamente, aplique o mesmo argumento ao par $a_2=77$ e $b_2=198$. A equação de Euclides nos dá $$198=77\times 2+44.$$

Por isso, $$\textrm{mdc}(77,198)=\textrm{mdc}(77,198-77\times 2)=\textrm{mdc}(77,44).$$

Mais uma vez, aplicamos o argumento ao par $a_3=44$ e $b_3=77$. Como $$77=44\times 1+33,$$ segue que $$\textrm{mdc}(44,77)=\textrm{mdc}(44,77-44\times 1)=\textrm{mdc}(44,33).$$

De novo, use o mesmo argumento ao par $a_4=33$ e $b_4=44$: $$44=33\times 1+11.$$ Assim, $$\textrm{mdc}(33,44)=\textrm{mdc}(33,44-33\times 1)=\textrm{mdc}(33,11).$$

Finalmente, se $a_5=11$ e $b_5=33$, temos que $33=11\times 3$ e

$$\textrm{mdc}(33,11)=\textrm{mdc}(33-11\times 3,11)=\textrm{mdc}(0,11)=11.$$

Portanto, $$\textrm{mdc}(4873, 275)=11.$$

Versão gráfica do método

Podemos apresentar o método acima de uma forma gráfica. Veja abaixo.

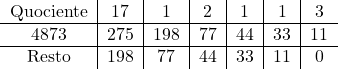
Observe que o quociente não nos interessa nesse algoritmo. Só precisamos do resto.

Problemas resolvidos sobre máximo divisor comum

Vejamos agora como se resolve problemas usando máximo divisor comum.

É uma ótima oportunidade para ver como é feita a interpretação dessas questões.

Problema 1

Voltemos mais um exemplo ao problema dos pedaços de pano.

Solução:

Nós já fizemos a interpretação dele e chegamos a conclusão que precisamos calcular $\textrm{mdc}(72, 90)$.

Vamos usar o método 2 para calcular esse mdc.

Multiplicando os fatores primos na coluna da direita, obtemos
$$\textrm{mdc}(72,90)=2\times 3\times 3=18.$$

Portanto, a largura das tiras deve ser de 18 polegadas.

Problema 2

(FCC) Um auxiliar de enfermagem pretende usar a menor quantidade possível de gavetas para acomodar 120 frascos de um tipo de medicamento, 150 frascos de outro tipo e 225 frascos de um terceiro tipo. Se ele colocar a mesma quantidade de frascos em todas as gavetas, e medicamentos de um único tipo em cada uma delas, quantas gavetas deverá usar?

a) 33.
b) 48.
c) 75.
d) 99.
e) 165.

Solução:

Vamos destacar alguns trechos do enunciado que merecem atenção:

“… menor quantidade possível de gavetas…”
“120 frascos de um tipo de medicamento, 150 frascos de outro tipo e 225 frascos de um terceiro tipo”
“…mesma quantidade de frascos em todas as gavetas e medicamentos de um único tipo em cada uma delas”.

O auxiliar de enfermagem pretende colocar frascos de medicamentos no menor número de gavetas possível.

Assim, cada gaveta deve conter o maior número possível de frascos.

Temos ainda que o número de frascos em cada gaveta deve ser o mesmo e que cada gaveta deve conter um único tipo de medicamento.

Portanto, o número de frascos em cada gaveta deve ser o máximo divisor comum de 120, 150 e 225 que são as quantidades de frascos especificadas no enunciado.

Vamos usar novamente o método 2 para calcular $\textrm{mdc}(120,150, 25)$.

Seguindo o método, temos

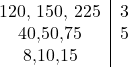
Logo, $\textrm{mdc}(120,150,225)=15$.

Portanto, o total de gavetas utilizadas será determinado pela divisão entre o total de frascos pela quantidade de frascos que serão acomodadas em cada gaveta.
$$\frac{120+150+225}{15}=8+10+15=33.$$