Frações impróprias são um tipo especial de frações onde o numerador é maior do que ou igual ao numerador. Essas frações estão relacionados com os números mistos que nada mais são do que uma combinação de um número inteiro e de uma fração própria.
Você sabia que os números $$\frac{401}{10}\quad\mbox{e}\quad 40\frac{1}{10}$$ são iguais?
Certamente, você já se deparou com números apresentados nessas duas formas em seus estudos sobre frações.
Mas o que eles significam e qual a relação entre eles? E como transformar um tipo no outro?
São essas perguntas que iremos responder ao longo deste artigo.
Por isso, continue a sua leitura para descobrir.
O que são frações impróprias?
Frações impróprias são frações onde o numerador é maior do que ou igual ao denominador.
Por outro lado, as frações próprias são aqueles em que o numerador é menor do que o denominador.
Dentre as frações impróprias temos as frações aparentes, que são aquelas frações que representam números inteiros. Ou seja, o denominador divide o numerador.
Assim, as frações $$\frac{7}{3}, \frac{1010}{255}\;\mbox{e}\; \frac{130}{111}$$ são frações impróprias, $$\frac{1}{122}, \frac{3}{7}\;\mbox{e}\;\frac{122}{123}$$
são frações próprias e $$\frac{39}{13}, \frac{100}{25}\;\mbox{e}\;\frac{503}{503}$$
são frações aparentes.
As figuras abaixo ilustram cada um dos tipos de frações.
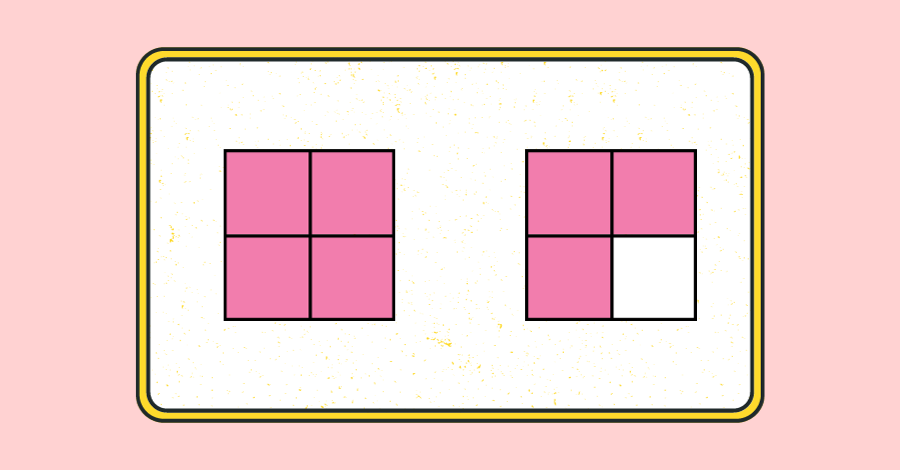
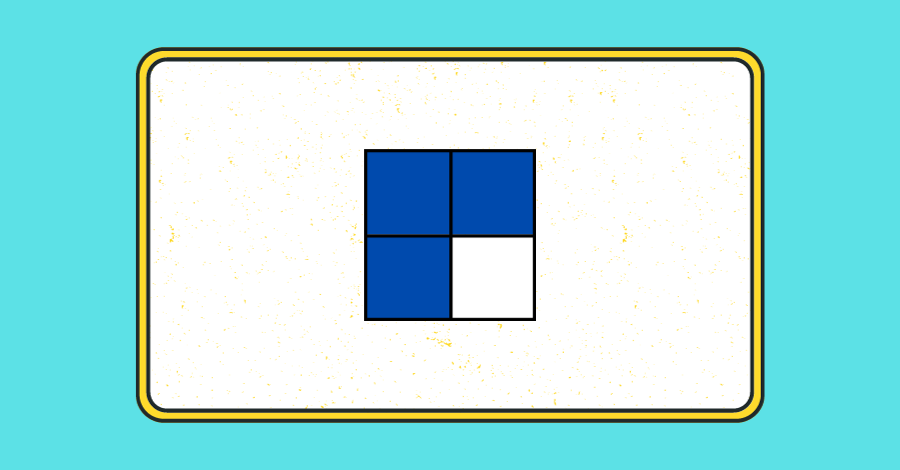
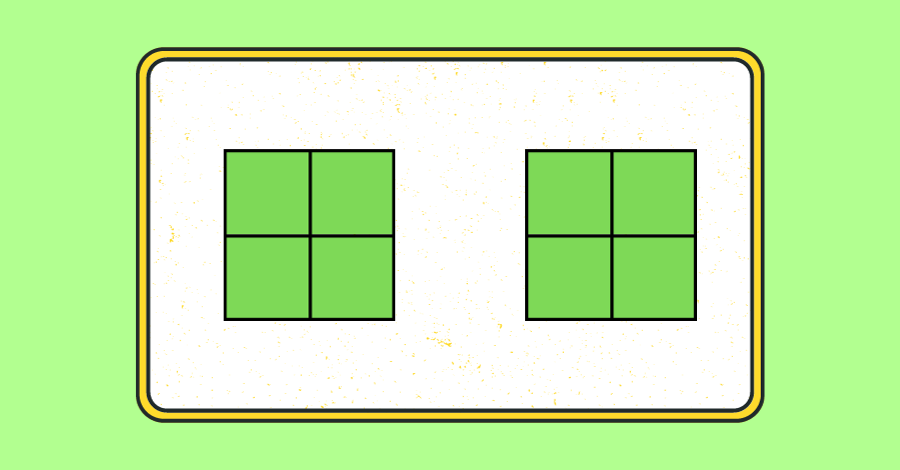
O que são números mistos?
Quando estudamos frações impróprias nos deparamos constantemente com os números mistos.
Os **números mistos** são números são uma combinação de número inteiro e de uma fração própria.
Eles são da forma $$1\frac{3}{4}, 3\frac{2}{5}\;\mbox{e}\;10\frac{17}{32}.$$
Dito de outro modo, eles são uma soma entre um número inteiro e uma fração própria.
Por exemplo, $1\dfrac{3}{4}$ é uma forma reduzida para $1+\dfrac{3}{4}$.
Além disso, esses números representam frações impróprias como ilustra a figura a seguir.

Assim, esses números são bastante úteis quando queremos identificar a posição de uma fração imprópria na reta numérica.
Por exemplo, o número misto $3\dfrac{2}{5}$ está entre $3$ e $4$.
Eles também podem ser de grande ajuda na hora de comparar frações. De fato, qual dos números a seguir é o maior $$\frac{11}{3}\;\mbox{ou}\;\frac{17}{4}?$$
O primeiro é igual a $3\dfrac{2}{3}$ e o segundo é igual a $4\dfrac{1}{4}$.
Portanto, $\dfrac{17}{4}$ é o maior.
Dessa forma, saber converter frações impróprias em números mistos (e vice-versa) é fundamental.
Convertendo frações impróprias em números mistos
Vejamos agora como transformar uma fração imprópria em um número misto.
Para fazer isso, dividimos o numerador pelo denominador.
Assim, o numerador é o dividendo e o denominador é o divisor.
Por isso, ao efetuarmos a divisão, obtemos um quociente e um resto.
O quociente será a parte inteira do número misto e o resto será o numerador da fração própria.
E o denominador dessa fração própria será o mesmo da fração original.
Em outras palavras, se $\dfrac{a}{b}$, com $a>b$, é uma fração imprópria, existem (únicos) inteiros $q$ e $0\leq r<b,$ tais que $$a=bq+r.$$ Assim, o número misto correspondente será $$q\frac{r}{b}.$$
Exemplo 1: Converta $\dfrac{19}{5}$ em um número misto.
Dividindo $19$ por $5$, obtemos $3$ com resto $4$.
Assim, seguindo o passo a passo acima obtemos $$\frac{19}{5}=3\frac{4}{5}.$$
Exemplo 2: Converta $\dfrac{47}{6}$ em um número misto.
Dividindo $47$ por $6$, obtemos $7$ com resto $5$.
Portanto, $$\frac{47}{6}=7\frac{5}{6}.$$
Convertendo números mistos em frações impróprias
Às vezes, é melhor usar a fração imprópria do que o número misto correspondente.
Isso porque a notação $q\dfrac{r}{b}$ pode representar um número misto e assim pode significar $q+\dfrac{r}{b}$ ou pode representar o produto $q\cdot \dfrac{r}{b}$.
Essa dúvida pode surgir quando formos efetuar algumas operações básicas, como por exemplo $$\frac{1}{3}+5\frac{2}{7}.$$
Por isso, devemos ter esse cuidado quando estivermos redigindo uma solução de uma questão.
Mas como eliminar essa dúvida?
Uma forma de fazer isso é convertendo o número misto em uma fração imprópria.
Para fazer essa conversão, basta seguir os seguintes passos simples:
- Multiplique a parte inteira pelo denominador;
- some o resultado obtido no passo anterior e some ao numerador;
- escreva o resultado obtido no último passo sobre o denominador.
A fração obtida será a fração imprópria correspondente.
Exemplo 3: Converta $4\dfrac{5}{8}$ em uma fração imprópria.
Seguindo os passos acima, temos
- $4\cdot 8=32$;
- $32+5=37$;
- $\dfrac{37}{8}$.
Assim, $$4\frac{5}{8}=\frac{37}{8}.$$
Exemplo 4: Converta $9\dfrac{2}{11}$ em uma fração imprópria.
Multiplicando a parte inteira pelo denominador obtemos $$9\cdot 11=99.$$
Em seguida, somamos esse número com o numerador: $$99+2=101.$$
Portanto, $$9\frac{2}{11}=\frac{101}{11}.$$
Uma outra maneira de fazer essa conversão é através da soma de frações. De fato, considere esse último exemplo.
Sabemos que $9\dfrac{2}{11}$ significa $9+\dfrac{2}{11}$. Com isso, temos $$9+\frac{2}{11}=\frac{99+2}{11}=\frac{101}{11}.$$
Conclusão
Vimos o que significam as frações impróprias e os números mistos.
Eles estão intimamente relacionados, uma vez que uma fração imprópria pode ser convertida em um número misto e vice-versa.
Por fim, vimos como cada uma dessas conversões são importantes em certos contextos.
O que você achou deste conteúdo?
Deixe um comentário abaixo se esse ele foi útil para você.


0 Comentários