Você já ficou em dúvida na hora de responder qual é o domínio ou a imagem de uma função? Ou ainda se perguntou o que é, de fato, o tal do contradomínio?
Muitos estudantes acabam se confundindo ao longo do aprendizado de funções, pois, embora os termos “domínio”, “contradomínio” e “imagem” sejam frequentemente usados, nem sempre fica claro como eles se diferenciam.
Essa falta de clareza pode gerar dificuldades tanto na resolução de exercícios quanto na realização de outros estudos, como a análise de gráficos de funções.
Neste artigo, você vai entender de vez o que são domínio, contradomínio e imagem de uma função, com explicações simples, exemplos visuais e dicas práticas.
Ao final, você será capaz de identificar esses conjuntos com clareza e segurança — seja resolvendo exercícios, lendo gráficos ou interpretando leis de formação.
O que é uma função?
Antes de começarmos a explorar o domínio, contradomínio e imagem de uma função, é importante relembrarmos o conceito de função.
De forma simples, uma função é uma correspondência entre dois conjuntos, em que cada elemento do primeiro conjunto, chamado de domínio, está associado a exatamente um elemento do segundo conjunto, chamado de contradomínio.
Imagine uma função como uma “máquina” que recebe um valor de entrada (do domínio), realiza uma operação e entrega um único resultado (no contradomínio).

Nem todo valor do contradomínio precisa necessariamente ser atingido pela função — e é aí que entra o conceito de imagem, como veremos mais adiante.
Mas para deixar isso ainda mais claro, vamos agora formalizar o conceito de função, usando notações matemáticas.
Uma função $f$ de um conjunto $A$ em um conjunto $B$ é uma regra que associa cada elemento $a\in A$ a um único elemento $b\in B$. Nesse caso, escrevemos $b=f(a)$ e denotamos a função por $f: A\to B$.
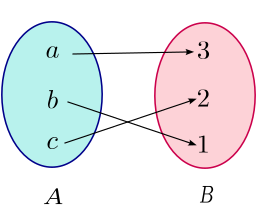
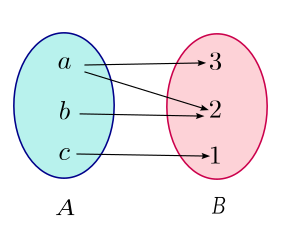
A seguir, você verá três diagramas ilustrando uma função e duas relações que não são funções:
Observe que todo elemento do conjunto $A$ está associado com um único elemento de $B$.
Esse diagrama ilustra uma relação que não é uma função, pois o elemento $a$ está associado com mais de um elemento de $B$, a saber, $2$ e $3$.

Novamente, temos uma relação que não é uma função, já que o conjunto $A$ possui em elemento que não está associado com elementos de $B$.
Essas distinções visuais ajudam a consolidar a definição de função de forma intuitiva.
O que é domínio de uma função?
O domínio de uma função é o conjunto de todos os valores de entrada possíveis. Ele reúne todos os elementos que entram na “máquina”.
Mais precisamente, o domínio de uma função $f$ de $A$ em $B$ é o conjunto $A$.
Exemplo: O domínio da função $f: \{a,b,c\}\to\{1,2,3\}$, dada por $f(a)=3, f(b)=1$ e $f(c)=2$, é o conjunto $\{a,b,c\}$.
Na maioria das vezes, apresenta-se uma função por meio de uma expressão algébrica que descreve como a saída depende da variável de entrada.
Porém, essa fórmula não revela tudo por si só: é fundamental considerar qual é o conjunto de valores que podem ser usados como entrada — ou seja, o domínio da função.
Em muitos casos, o domínio não vem explicitamente indicado, e cabe a nós determiná-lo com base na própria expressão da função.
Isso é o que chamamos de domínio natural — o conjunto de todos os valores para os quais a fórmula faz sentido matematicamente.
O domínio natural de uma função
Quando uma função é apresentada por uma expressão algébrica envolvendo variáveis reais, e o domínio não é especificado de forma explícita, consideramos por padrão o domínio natural da função.
Esse domínio é o conjunto de todos os valores reais para os quais a fórmula da função está bem definida — ou seja, para os quais não ocorrem operações inválidas, como:
- Divisão por zero, que não tem resultado definido.
- Raiz de índice par de número negativo, que não está nos reais.
Vamos ver alguns exemplos para ilustrar como determinar o domínio natural.
Exemplo 1: \( f(x) = \frac{1}{x} \)
Neste caso, a função está definida para todo número real exceto quando \( x = 0 \), pois não é possível dividir por zero.
Portanto, o domínio natural é
\[
\mathbb{R} \setminus \{0\}
\]
Exemplo 2: \( f(x) = \sqrt{x-2} \)
A raiz quadrada só está definida para números maiores ou iguais a zero. Portanto, o valor dentro da raiz precisa satisfazer:
\[
x-2 \geq 0 \Rightarrow x \geq 2
\]
Logo, o domínio natural é
\[
[2, \infty)
\]
Exemplo 3: \( f(x) = \frac{1}{\sqrt{x-1}} \)
Aqui, temos duas restrições ao mesmo tempo:
- o índice do radical é par, o que exige que $x-1\geq 0$ e
- $\sqrt{x-1}$ está no denominador de uma fração, o que requer $x-1\neq 0.$
Portanto:
\[
x-1 > 0 \Rightarrow x > 1
\]
e o domínio natural é
\[
(1, \infty).
\]
Exemplo 4: \( f(x) = \sqrt{x^2-4} \)
Como temos uma raiz quadrada, o radicando precisa ser maior ou igual a zero:
\[
x^2-4 \geq 0
\]
Resolvendo a inequação, obtemos
\[
x^2 \geq 4 \Rightarrow x \leq -2 \quad \text{ou} \quad x \geq 2
\]
Assim, o domínio natural dessa função é
\[
(-\infty, -2] \cup [2, \infty)
\]
O que é o contradomínio de uma função?
O contradomínio de uma função é o conjunto no qual a função toma seus valores.
Ele é conhecido como o conjunto de chegada, ou seja, o conjunto em que os valores da função devem estar.
Mais precisamente, se temos uma função $f: A\to B$, o contradomínio de $f$ é o conjunto $B$.
Vale destacar que nem todo elemento do contradomínio precisa estar associado a algum valor do domínio por meio da função. Isto é, a função nem sempre assume todos os valores presentes no contradomínio.
Por exemplo, considere a função $f:\mathbb{R}\to \mathbb{R}$, dada por $f(x)=x^2$.
O contradomínio dessa função é $\mathbb{R}$, porém ela nunca produz valores negativos como resultado.
Isso significa que valores como \( -1\) e \( -9 \), que estão no contradomínio, não são atingidos pela função, pois não existe nenhum \( x \in \mathbb{R} \) tal que \( f(x) = -1 \) ou \( f(x) = -9 \).
O que é a imagem de uma função?
A imagem de uma função é o conjunto de todos os valores atingidos pela função, ou seja, o conjunto de todos os resultados que a função produz.
A imagem é, portanto, um subconjunto do contradomínio.
Em símbolos matemáticos, a imagem de uma função $f: A\to B$ é o conjunto $$\operatorname{Im}(f)=\{b\in B; b=f(a), \text{para algum $a\in A$}\}.$$
Exemplo: Considere a a função $f:\{2,5,7\}\to \{1,2,10\}$, dada por $f(2)=1, f(5)=10$ e $f(7)=10$. A imagem dessa função é $\operatorname{Im}(f)=\{1,10\}$.
Esse exemplo mostra que a imagem e o contradomínio podem ser conjuntos diferentes.
Exemplos com funções reais
Vamos ver agora como determinar a imagem de algumas funções reais, ou seja, funções do tipo \( f: \mathbb{R} \to \mathbb{R} \).
1. \( f(x) = x^2 \)
Os valores de saída (isto é, os valores de \( f(x) )\) nunca são negativos, já que o quadrado de qualquer número real é maior ou igual a zero. Assim:
\[
\operatorname{Im}(f) = [0, +\infty).
\]
2. \( f(x) = \sqrt{x-1} \)
Como \( f(x) = \sqrt{x-1} \), os valores possíveis de saída também são não negativos. Quando \( x = 1 \), temos \( f(1) = 0 \), e à medida que \( x \) cresce, \( f(x) \) também cresce. Logo:
\[
\operatorname{Im}(f) = [0, +\infty).
\]
3. \( f(x) = \dfrac{1}{x^2 + 1} \)
Note que o menor valor que \( x^2 \) pode assumir é 0, quando \( x = 0 \). Assim, o maior valor que a função pode atingir é:
\[
f(0) = \frac{1}{0^2 + 1} = 1.
\]
Por outro lado, à medida que \( |x| \) aumenta, \( x^2 \) cresce e, portanto, \( f(x) = \frac{1}{x^2 + 1} \) se aproxima de 0 (mas nunca atinge 0). Portanto, a imagem da função está no intervalo:
\[
\operatorname{Im}(f) = (0, 1].\]
Conclusão
Agora que você conhece as diferenças entre domínio, contradomínio e imagem, pode resolver exercícios com mais confiança e clareza.
Lembre-se de que domínio está relacionado aos valores de entrada, contradomínio ao conjunto de saída possível, e imagem àqueles valores de saída que realmente podem ser atingidos pela função.
Não deixe de praticar, pois a prática é essencial para a fixação desses conceitos!



0 Comentários