As derivadas parciais abordam o problema da variação de uma função em relação a uma única variável enquanto todas as outras variáveis são mantidas constantes.
Isso se torna de extrema utilidade quando lidamos com fenômenos que dependem de várias grandezas inter-relacionadas.
Neste artigo, veremos o que são derivadas parciais, a interpretação geométrica delas e como calculá-las aplicando as regras de derivação de funções de uma variável
Funções de duas variáveis
Antes de entendermos o que é derivada parcial, vamos falar primeiro de funções de duas variáveis.
Uma função de duas variáveis $f$ é uma regra que associa a cada par ordenado de números reais $(x,y)$ de um conjunto de $D$, um número real $f(x,y)$
Por exemplo, se $x$ e $y$ são o comprimento e a largura de um retângulo, a área desse retângulo é dada por $$A=A(x,y)=xy.$$
Ou seja, $A$ é uma função de duas variáveis.
O conjunto $D$ é chamado de domínio e o conjunto $\mbox{Im}(f):=\{f(x,y)\in\mathbb{R}; (x,y)\in D\}$ é chamada de imagem de $f$.
Escrevendo $z=f(x,y)$, as variáveis $x,y$ são chamadas de variáveis independentes e $z$ de variável dependente.
Quando não explicitado, o domínio de uma função é o maior conjunto para o qual a regra de definição gera números reais.
O que é derivada parcial?
Sejam $f: D\subseteq \mathbb{R}^2\to \mathbb{R}$ uma função e $(x_0,y_0)\in D$. Fixe $y_0$ e considere a função $g$ de uma variável dada por $$g(x)=f(x,y_0).$$
A derivada de $g$ em $x_0$ (caso exista) é chamada de derivada parcial de $f$ em relação a $x$ no ponto $(x_0,y_0)$.
As notações mais utilizadas para derivada parcial em relação a $x$ são $$\frac{\partial f}{\partial x}(x_0,y_0), f_x(x_0,y_0).$$
Dessa forma, $\dfrac{\partial f}{\partial x}(x_0,y_0)=g'(x_0)$. Pela definição de derivada $$\frac{\partial f}{\partial x}(x_0,y_0)=g'(x_0)=\lim_{x\to x_0}\frac{g(x)-g(x_0)}{x-x_0},$$ ou seja, $$\frac{\partial f}{\partial x}(x_0,y_0)=\lim_{x\to x_0}\frac{f(x,y_0)-f(x_0,y_0)}{x-x_0},$$
ou ainda,
$$\frac{\partial f}{\partial x}(x_0,y_0)=\lim_{h\to 0}\frac{f(x_0+h,y_0)-f(x_0,y_0)}{h}.$$
Seja $$A=\{(x,y)\in D; f_x(x,y)\;\mbox{existe}\}.$$
Assim, temos uma nova função, indicada por $\dfrac{\partial f}{\partial x}$ ou por $f_x$ e definida em $A$, que a cada $(x,y)\in A$ associa o número $\dfrac{\partial f}{\partial x}(x,y),$ onde $$\frac{\partial f}{\partial x}(x,y)=\lim_{h\to 0}\frac{f(x+h,y)-f(x,y)}{h}.$$
Essa função é chamada de função derivada parcial de 1ª ordem de $f$, em relação a $x$, ou derivada parcial de $f$ em relação a $x$.
Da mesma forma, definimos a derivada parcial de $f$ em relação a $y$, no ponto $(x_0,y_0)$ que se indica por $\dfrac{\partial f}{\partial y}$: $$\frac{\partial f}{\partial y}(x_0,y_0)=\lim_{y\to y_0}\frac{f(x_0,y)-f(x_0,y_0)}{y-y_0},$$ ou $$\frac{\partial f}{\partial y}(x_0,y_0)=\lim_{h\to 0}\frac{f(x_0,y_0+h)-f(x_0,y_0)}{h}.$$
Em outras palavras, $f_x(x,y)$ é a derivada em relação a $x$, de $f(x,y)$, mantendo-se $y$ constante.
Por outro lado, $f_y(x,y)$ é a derivada de $f(x,y)$ em relação a $y$, mantendo-se $x$ constante.
Exemplo 1: Se $f(x,y)=2x^3y^5+y\;\mbox{sen}\; x$, determine $f_x(1,0)$ e $f_y(1,0)$.
Solução: Mantendo $y$ constante e derivando em relação a $x$, obtemos $f_x(x,y)=6x^2y^5+y\cos x$ e assim $$f_x(1,0)=6\cdot 1^2\cdot 0^5+0\cdot \cos 1=0.$$
Mantendo $x$ constante e derivando em relação a $y$ obtemos $f_y(x,y)=10x^3y^4+\mbox{sen}\; x$ e assim $f_y(1,0)=\mbox{sen}\;1$.
Exemplo 2: Se $f(x,y)=\ln (x^2+y^2+1)$, calcule $f_x(x,y)$ e $f_y(x,y)$.
Solução: Usando a regra da cadeia para funções de uma variável, temos $$\small f_x(x,y)=\frac{1}{x^2+y^2+1}\cdot\frac{\partial}{\partial x}(x^2+y^2+1)=\frac{2x}{x^2+y^2+1}$$ e $$\small f_y(x,y)=\frac{1}{x^2+y^2+1}\cdot\frac{\partial}{\partial y}(x^2+y^2+1)=\frac{2y}{x^2+y^2+1}.$$
Interpretação geométrica das derivadas parciais
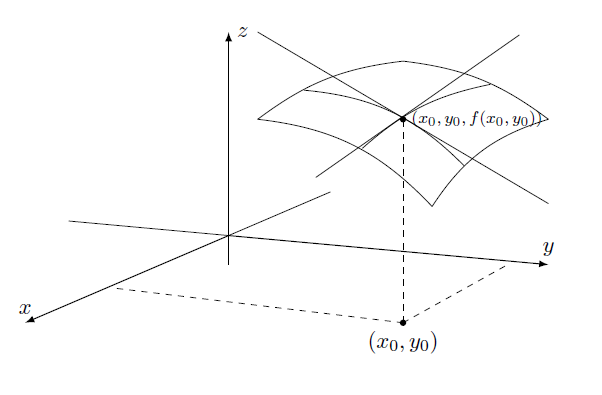
As derivadas parciais em um ponto $P=(x_0,y_0)$ são inclinações das retas tangentes no ponto $(x_0,y_0,f(x_0,y_0))$ das curvas obtidas pelas interseções dos planos $y=y_0$ e $x=x_0$ com o gráfico de $f$ como mostra a figura abaixo.
Derivadas parciais de funções com mais de duas variáveis
Derivadas parciais são definidas para funções de qualquer número de variáveis.
De fato, seja $f:U\subseteq \mathbb{R}^n\to \mathbb{R}$ uma função de $n$ variáveis $x_1, x_2,\ldots, x_n$.
A derivada parcial de $f$ em relação a variável $x_i$ é $$\small\frac{\partial f}{\partial x_i}=\lim_{h\to 0}\frac{f(x_1,\ldots,x_i+h,\ldots,x_n)-f(x_1,\ldots,x_i,\ldots,x_n)}{h}.$$Na prática, calculamos a derivada (de uma variável) em relação a $x_i$ tratando as outras variáveis como constantes.
Exemplo 3: Seja $f(x,y,z,w)=\dfrac{e^{x^2z-y^4}}{z+w^3}$. Calcule $f_z(0,0,1,0)$.
Solução: Use as regras do quociente e da cadeia, tratando $x,y$ e $w$ como constantes $$f_z(x,y,z,w)=\frac{x^2(z+w^3)e^{x^2z-y^4}-e^{x^2z-y^4}}{(z+w^3)}.$$
Daí, $$f_z(0,0,1,0)=\frac{1-1}{1}=0.$$
Derivadas Parciais de Ordem Superior
As derivadas parciais de ordem superior são derivadas de derivadas.
As derivadas de segunda ordem de $f$ são
$$(f_x)_x=f_{xx}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2 f}{\partial x^2}$$
$$(f_x)_y=f_{xy}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial x}\right)=\frac{\partial^2f}{\partial y\; \partial x}$$
$$(f_y)_x=f_{yx}=\frac{\partial}{\partial x}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial x\; \partial y}$$
$$(f_y)_y=f_{yy}=\frac{\partial}{\partial y}\left(\frac{\partial f}{\partial y}\right)=\frac{\partial^2f}{\partial y^2}.$$
Exemplo 4: Calcule as derivadas parciais de 2ª ordem $$f(x,y)=x^3+y^2e^x.$$
Solução: Primeiro, calculamos as derivadas de 1ª ordem: $$f_x(x,y)=3x^2+y^2e^x$$ e $$f_y(x,y)=2ye^x.$$
Em seguida, calculamos as derivadas de 2ª ordem:
$$f_{xx}(x,y)=6x+y^2e^x\quad \mbox{e}\quad f_{xy}(x,y)=2ye^x$$ $$f_{yx}(x,y)=2ye^x\quad\mbox{e}\quad f_{yy}(x,y)=2e^x.$$
Note que no exemplo anterior temos $f_{xy}=f_{yx}$. Veremos a seguir em quais condições isso sempre acontece.
Teorema de Clairaut: Suponha que $f$ seja definida em um conjunto aberto $U\subseteq \mathbb{R}^2$. Se $f_{xy}$ e $f_{yx}$ são contínuas em $U$, então $$f_{xy}(x,y)=f_{yx}(x,y)$$ para todo $(x,y)\in U$.
Exemplo 5: Calcule $\dfrac{\partial^2 f}{\partial x\;\partial y}$, onde $$f(x,y)=xy+\frac{e^y}{y^2+1}.$$
Solução: O símbolo $\dfrac{\partial^2 f}{\partial x\;\partial y}$ nos diz que derivamos primeiro com respeito a $y$ e em seguida em relação a $x$.
No entanto, se invertemos a ordem de derivação chegamos a resposta mais rapidamente.
Temos $$\frac{\partial f}{\partial x}= y\quad \mbox{e}\quad \frac{\partial^2 f}{\partial y\;\partial x}=1.$$




0 Comentários