A derivação implícita é uma técnica importante no cálculo diferencial que permite encontrar as derivadas de funções implícitas, onde a variável dependente não pode ser expressa explicitamente em termos da variável independente.
Essa técnica é extremamente útil em diversos campos, desde a física até a economia.

Neste artigo, vamos explorar passo a passo como resolver problemas de derivação implícita, fornecendo uma abordagem clara e prática para o processo.
Entendendo a derivação implícita
Se você está aqui, é porque já deve saber como calcular $\dfrac{dy}{dx}$ quando $y$ é dado explicitamente como uma função de $x$, como por exemplo em \[y=x^2+2x-4.\]
Mas, o que fazer quando $y$ é dado implicitamente, como por exemplo em \[y^3+xy=x^2-1?\]
O que devemos fazer é encontrar um método que usa as regras de derivação que já conhecemos para determinar $\dfrac{dy}{dx}$.
Esse é o método da derivação implícita.
Identificando as variáveis
No contexto que estamos trabalhando, temos duas variáveis, $x$ e $y$.
Na maioria das vezes, tratamos $y$ como uma função de $x$. Nesse caso, dizemos que $x$ é a variável independente e $y$ é a variável dependente.
Derivando Implicitamente
Mostraremos agora como fazer a derivação implícita. Voltemos para o exemplo que demos inicialmente, ou seja, vamos determinar $\dfrac{dy}{dx}$ onde $y$ é dado implicitamente por \[y^3+xy=x^2-1.\]
Para fazer isso, dividimos o cálculo em dois passos.
Passo 1: Derive ambos os lados em relação a $x$.
\[\frac{d}{dx}(y^3+xy)=\frac{d}{dx}(x^2-1)\] \[\frac{d}{dx}(y^3)+\frac{d}{dx}(xy)=2x.\]
Agora, como lidar com os termos $\dfrac{d}{dx}(y^3)$ e $\dfrac{d}{dx}(xy)$?
Usaremos a Regra da Cadeia e a Regra do Produto, respectivamente.
Considerando $y$ como uma função de $x$, temos \[\frac{d}{dx}(y^3)=3y^2\frac{dy}{dx}\;\mbox{e}\;\frac{d}{dx}(xy)=y+x\frac{dy}{dx}.\]
Daí e de $\frac{d}{dx}(y^3)+\frac{d}{dx}(xy)=2x$, segue que \[3y^2\frac{dy}{dx}+y+x\frac{dy}{dx}=2x.\]
Passo 2: Isole $\dfrac{dy}{dx}$.
Coloque os termos envolvendo $\dfrac{dy}{dx}$ no lado esquerdo da equação e o demais termos no lado direito.
\[3y^2\frac{dy}{dx}+x\frac{dy}{dx}=2x-y\]\[ (3y^2+x)\frac{dy}{dx}=2x-y\Rightarrow \frac{dy}{dx}=\frac{2x-y}{3y^2+x}.\]
Resolvendo problemas
Usaremos o que aprendemos até agora para resolver vários problemas.
Problema 1. Considere a curva descrita pela equação $x^3+y^3=3xy$ e ilustrada na figura abaixo.
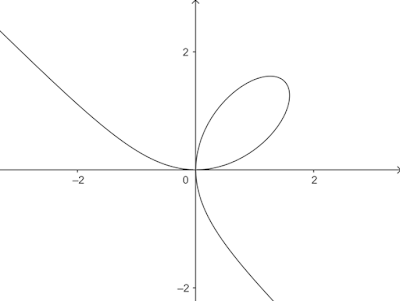
(a) Encontre uma equação da reta tangente a essa curva no ponto $\left(\frac{3}{2},\frac{3}{2}\right)$.
(b) Encontre um ponto da curva diferente da origem no qual a reta tangente é horizontal.
Solução:
(a) Primeiramente, devemos encontrar $\dfrac{dy}{dx}$ em $\left(\frac{3}{2},\frac{3}{2}\right).$
Para isso, faremos derivação implícita.
Seguindo o procedimento acima, temos \[3x^2+3y^2\frac{dy}{dx}=3(y+x\frac{dy}{dx}).\] Daí, obtemos \[3\frac{dy}{dx}(y^2-x)=3(y-x^2)\Rightarrow \frac{dy}{dx}=\frac{y-x^2}{y^2-x}.\]
Para calcular a derivada em $\left(\frac{3}{2},\frac{3}{2}\right)$, substituímos $x=\frac{3}{2}$ e $y=\frac{3}{2}$ na última igualdade. \[\frac{dy}{dx}\Big|_{(\frac{3}{2},\frac{3}{2})}=\frac{\frac{3}{2}-\frac{9}{4}}{\frac{9}{4}-\frac{3}{2}}=-1.\]
Portanto, a equação da reta tangente à curva no ponto $\left(\frac{3}{2},\frac{3}{2}\right)$ é \[y-\frac{3}{2}=-1\left(x-\frac{3}{2}\right)\Rightarrow y=-x+3.\]
(b) Queremos encontrar um ponto $P$ para o qual $\frac{dy}{dx}\Big|_P=0.$ Para isso, faça
\[\frac{dy}{dx}=\frac{y-x^2}{y^2-x}=0\] para obter $y=x^2$.
Como esse ponto pertence à curva, substitua $y=x^2$ em $x^3+y^3=3xy$. Além disso, queremos que ele seja diferente de $(0,0)$, assim, devemos ter $x\neq 0$.
Com isso, temos \[x^3+x^6=3x^3\Rightarrow x^3=2,\] ou seja, $x=\sqrt[3]{2}$ e, por conseguinte, $y=\sqrt[3]{4}$.
Logo, o ponto onde a reta tangente é horizontal é $(\sqrt[3]{2},\sqrt[3]{4})$.
Problema 2. Considere as seguintes equações
$x^2+y^2=25$
$x^2-xy+y^2=13$
(a) Encontre as coordenadas dos pontos de interseção entre as duas curvas.
(b) Determine as inclinações da retas tangentes à curva dada pela segunda equação nos pontos obtidos no item (a).
Solução:
(a) Substituindo $x^2+y^2=25$ na segunda equação, obtemos \[25-xy=13\Rightarrow xy=12.\] Agora, como $(x+y)^2=x^2+y^2+2xy$, temos que $(x+y)^2=25+24=49$ o que implica que $x+y=\pm 7$.
Dessa forma, obtemos os seguintes sistemas de equações:
$$\left\{\begin{array}{l}
x+y=7 \\
xy=12
\end{array}\right.$$
e
$$\left\{\begin{array}{l}
x+y=-7 \\
xy=12
\end{array}\right.$$
Logo, os pontos de interseção são $(3,4), (4,3), (-3,-4)$ e $(-4,-3)$.
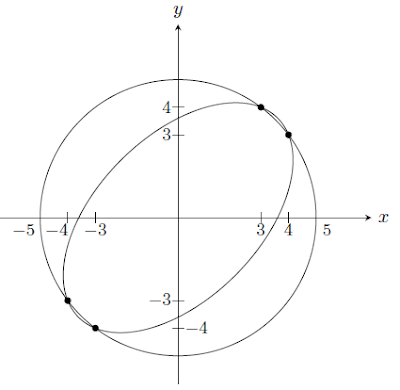
(b) Queremos determinar $\frac{dy}{dx}$ em $(3,4), (4,3), (-3,-4)$ e $(-4,-3)$, onde $y$ é dada implicitamente por \[x^2-xy+y^2=13.\]
Derivando ambos os membros da equação em relação a $x$, obtemos \[2x-\left(y+x\frac{dy}{dx}\right)+2y\frac{dy}{dx}=0,\] o que implica \[(2y-x)\frac{dy}{dx}=y-2x\Rightarrow \frac{dy}{dx}=\frac{y-2x}{2y-x}.\]
Assim, \[\frac{dy}{dx}\Big|_{(3,4)}=\frac{dy}{dx}\Big|_{(-3,-4)}=-\frac{2}{5}\] e \[\frac{dy}{dx}\Big|_{(4,3)}=\frac{dy}{dx}\Big|_{(-4,-3)}=-\frac{5}{2}.\]
Conclusão
A derivação implícita é uma ferramenta poderosa no campo do cálculo diferencial, permitindo-nos encontrar derivadas de funções implícitas em casos em que a forma explícita das equações não é facilmente obtida.
Ao aplicar a técnica da derivação implícita, pudemos abordar alguns problemas, como a interseção de curvas. A habilidade de calcular derivadas de funções implícitas nos fornece uma vantagem valiosa na resolução de uma ampla gama de problemas em matemática, física, economia e engenharia.
Portanto, ao dominar a derivação implícita, não apenas expandimos nosso conhecimento em matemática, mas também aumentamos nossa capacidade de resolver problemas do mundo real com precisão e eficiência.


0 Comentários