Como Resolver Sistemas de Equações do 1º Grau

Você gostaria de saber como resolver sistemas de equações do 1º grau e usá-los para resolver problemas matemáticos?

O que é um sistema de equações do 1º grau?

É uma coleção de uma ou mais equações envolvendo o mesmo conjunto de variáveis.

O objetivo em um exercício ou problema sobre sistemas de equações é encontrar os valores que satisfazem todas as equações do sistemas.

E para fazer isso, você precisa de um método.

Felizmente, existem vários métodos para resolver um sistema de equações do 1º grau, dentre os quais você pode escolher o que for mais conveniente para você.

Por fim, um desafio que pode surgir ao se estudar sistemas de equações é a interpretação dos enunciados dos problemas.

Extrair do texto quais são as condições satisfeitas pelos valores a serem descobertos e montar um sistema é um desafio para várias pessoas.

Se você está nessa situação, não se preocupe, é só continuar lendo para saber como resolver um sistema de equações do 1º grau e conhecer um passo a passo para montar um sistema de forma correta em um problema matemático.

O que é uma equação do 1º grau com duas variáveis?

Uma equação do 1º grau (ou equação linear) com duas variáveis é uma equação que pode ser escrita na forma $$ax+by=c,$$ onde $a$ e $b$ não são ambos iguais a zero.

Por exemplo, as equações

• $3x-2y=6$.
• $\dfrac{x}{5}+y=10$.
• $3x-4=4y+x-2$

são equações do 1º grau com duas variáveis.

Já as equações

• $x^3-2y=5$
• $2xy=100$

são equações com duas variáveis, mas não são equações do 1º grau.

O que é uma solução de uma equação de 1º grau com duas variáveis?

Uma solução da equação $$ax+by=c$$ é um par ordenado $(x,y)$ que torna essa igualdade verdadeira.

Por exemplo, o par ordenado $(1,2)$ é solução para a equação $$3x-y=1.$$

De fato, substituindo $x$ por 1 e $y$ por 2, obtemos $$3\cdot 1-2=3-2=1.$$

Por outro lado, o par $(0,0)$ não é uma solução dessa equação, pois $$3\cdot 0-0=0\neq 1.$$

Dependendo do universo, uma equação do 1º grau com duas variáveis pode ter finitas ou infinitas soluções.

Por exemplo, as soluções para $$x+y=3,\;\textrm{onde}\;(x,y)\in\mathbb{N}\times \mathbb{N}$$ são $(1,2)$, $(2,1).$

Mas se $(x,y)\in\mathbb{R}\times \mathbb{R}$, $$x+y=3$$ tem infinitas soluções.

Graficamente, as soluções de $ax+by=c$, com $(x,y)\in\mathbb{R}\times \mathbb{R}$ formam uma reta no plano cartesiano.

Em outras palavras, o conjunto de pares ordenados que satisfazem a equação $ax+by=c$ é o gráfico de $ax+by=c$.

O que é um sistema de equações de 1º grau com duas variáveis?

Um sistema de equações do 1º grau com duas variáveis é um conjunto de duas ou mais equações do 1º grau com duas variáveis.

Aqui vamos ver aqui sistemas com apenas duas equações. Ou seja, sistemas da forma

$$\left\{\begin{array}{l}
ax+by=c \\
dx+ey=f.
\end{array}\right.$$

O que é uma solução de um sistema?

Uma solução do sistema de equações do 1° grau

$$\left\{\begin{array}{l}
ax+by=c \\
dx+ey=f.
\end{array}\right.$$

é um par ordenado $(x,y)$ que é solução de ambas as equações $ax+by=c$ e $dx+ey=f.$

Por exemplo, o par ordenado $(3,1)$ é solução do sistema

$$\left\{\begin{array}{l}
x+y=4 \\
x-y=1.
\end{array}\right.,$$

pois substituindo $x$ por 3 e $y$ por 1 temos $$3+1=4$$ e $$3-1=2.$$

Por outro lado, o par $(2,2)$ não é solução desse sistema, pois ele não é solução da 2ª equação $x-y=1$.

Quanto ao número de soluções, um sistema pode ser de 3 tipos.

Tipo 1: Sistema possível e determinado

O sistema possível e determinado é o sistema que possui uma única solução.

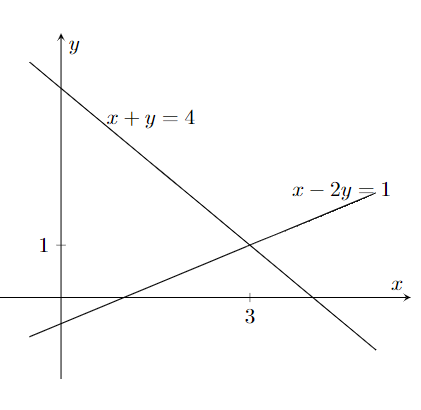
Um exemplo desse tipo é o sistema

$$\left\{\begin{array}{l}
x-2y=1 \\
x+y=4.
\end{array}\right.$$

Geometricamente, a solução de um sistema possível e determinado é o ponto de intersecção das retas determinadas por cada uma das equações do sistema.

Tipo 2: Sistema possível e indeterminado

O sistema possível e indeterminado é o sistema que possui infinitas soluções.

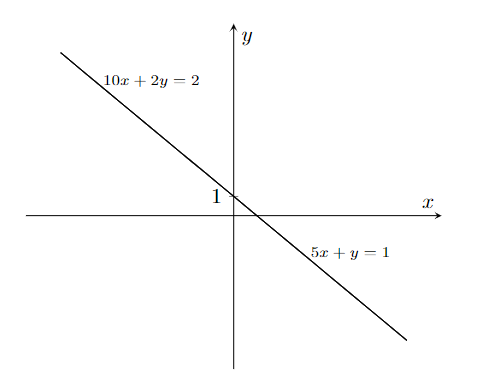
Por exemplo, o sistema

$$\left\{\begin{array}{c}
5x+y=1 \\
10x+2y=2.
\end{array}\right.$$

é um sistema possível e indeterminado, pois possui infinitas soluções. E essas soluções são elementos do conjunto $$\{(x,1-5x)\in\mathbb{R}^2; x\in\mathbb{R}\}.$$

Algumas das soluções são $(0,1), (\frac{1}{5},0), (-1,6), (2,-9),$ etc.

Geometricamente, as equações $5x+y=1$ e $10x+2y=2$ representam a mesma reta e as soluções do sistema possível e indeterminado são todos os pontos dessa reta.

Tipo 3: Sistema impossível

O sistema impossível é o sistema que não possui solução.

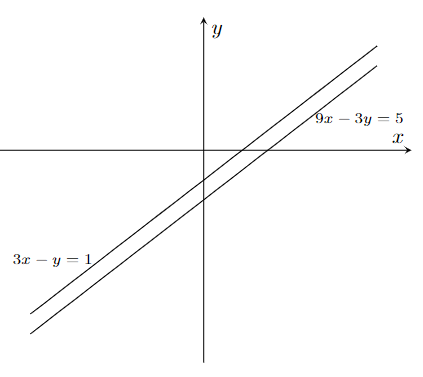
Um exemplo de um sistema desse tipo é o seguinte:

$$\left\{\begin{array}{c}
3x-y=1 \\
9x-3y=5.
\end{array}\right.$$

Esse sistema não possui solução.

De fato, se esse sistema possuísse uma solução $(x_0,y_0)$, então $$3x_0-y_0=1$$ e $$9x_0-3y_0=5.$$

Por outro lado, teríamos $$9x_0-3y_0=3(3x_0-y_0)=3\cdot 1=3,$$ o que implica que $3=5$, o que não é verdade.

Geometricamente, as retas determinadas pelas equações de um sistema impossível são paralelas e, portanto, não há pontos de intersecção.

Mas como saber se um sistema é possível determinado, possível indeterminado ou impossível?

Não é preciso resolver um sistema de equações para saber se ele é possível e determinado, possível e indeterminado ou impossível.

Para descobrir isso, você precisa olhar para os coeficientes das equações do sistema.

Considere então o sistema

$$\left\{\begin{array}{c}
ax+by=c \\
dx+ey=f.
\end{array}\right.$$

Se $$\frac{a}{d}\neq\frac{b}{e}, \quad d,e\neq 0$$ então o sistema é possível e determinado. Olhando para o nosso exemplo

$$\left\{\begin{array}{c}
x-2y=1 \\
x+y=4.
\end{array}\right.$$

percebemos que $$\frac{1}{1}\neq \frac{-2}{1}.$$ Logo, esse sistema é possível e determinado, possuindo apenas uma solução.

• Se $$\frac{a}{d}=\frac{b}{e}=\frac{c}{f}, \quad d,e,f\neq 0,$$ então o sistema é possível e indeterminado. No exemplo que vimos acima, temos $$\frac{5}{10}=\frac{1}{2}=\frac{1}{2}.$$
• E se $$\frac{a}{d}=\frac{b}{e}\neq \frac{c}{f}, \quad d, e, f\neq 0,$$ então o sistema é impossível. No nosso caso, temos $$\frac{3}{9}=\frac{-1}{-3}\neq \frac{1}{5}.$$

Vamos ver agora alguns métodos para descobrir as soluções desses sistemas.

03 métodos para resolver sistemas de equações do 1º grau com duas variáveis

Vejamos agora como resolver um sistema de equações do 1º grau de duas variáveis de 3 formas diferentes.

Eu vou te mostrar cada um dos métodos na prática.

Método da Substituição

Considere o sistema a seguir

$$\left\{\begin{array}{c}
4x-y=1 \\
x+y=4.
\end{array}\right.$$

Como resolver esse sistema usando o método da substituição?

1º passo: Escolha uma das equações.

Vamos escolher aqui a 2ª equação: $$x+y=4.$$

2º passo: Isole uma das variáveis.

Vamos isolar aqui a variável $y$. Ou seja, $$y=4-x.$$

3º passo: Substitua a variável pela expressão encontrada na outra equação para obter uma equação do 1º grau em uma variável.

No nosso caso vamos substituir $y$ por $4-x$ na 1ª equação. Obtemos$$4x-(4-x)=1.$$
4º passo: Resolva a equação obtida.

Vamos resolver então $$4x-(4-x)=1.$$ Essa equação é equivalente a $$4x-4+x=1\Rightarrow 5x=5,$$ donde segue que $$x=1.$$
5º passo: Substitua o valor encontrado em qualquer uma das equações para obter uma equação do 1º grau na outra variável.

Vamos substituir $x=1$ na 2ª equação para obter $$1+y=4.$$

6º passo: Resolva a equação obtida.

Resolvendo $$1+y=4,$$ obtemos $$y=3.$$
7º passo: Faça a verificação. Para fazer isso, substitua os valores encontrados em cada uma das equações e veja se elas são satisfeitas.

Fazendo isso no nosso caso, temos $$4\cdot 1-3=4-3=1$$ e $$1+3=4.$$

Portanto, a solução do sistema

$$\left\{\begin{array}{c}
4x-y=1 \\
x+y=4.
\end{array}\right. $$

é o par ordenado $(1,3)$.

Método da Adição

Se em ambas as equações, uma variável tiver coeficientes de mesmo valor absoluto, mas de sinais opostos, podemos usar o método da adição para resolver esse sistema.

O exemplo anterior é um sistema nessa situação. De fato, em

$$\left\{\begin{array}{c}
4x-y=1 \\
x+y=4.
\end{array}\right. $$

temos que os coeficientes de $y$ nas equações são $-1$ e $1$.

Assim, podemos aplicar o método da adição.

1º passo: Some as equações para eliminar uma das variáveis.

Fazendo isso no nosso caso, temos $$(4x-y)+(x+y)=1+4,$$ o que implica $$5x=5.$$
2º passo: Resolva a equação obtida.

Resolvendo a nossa equação obtemos $$x=1.$$

3º passo: Substitua o valor encontrado em uma das equações, obtendo uma equação do 1º grau na outra variável.

Vamos substituir na 1ª equação dessa vez.

Fazendo isso, obtemos $$4\cdot 1-y=1\Rightarrow 4-y=1.$$

4º passo: Resolva a equação obtida.

Resolvendo $4-y=1$, encontramos $y=3$.
5º passo: Faça a verificação.

Podemos aplicar o método da adição a qualquer sistema, mesmo quando os coeficientes de uma variável sejam de módulos diferentes.

Veja o exemplo a seguir.

Vamos resolver o sistema

$$\left\{\begin{array}{c}
3x-2y=1 \\
2x+5y=7.
\end{array}\right. $$

usando o método da adição.

Como você pode observar que tanto os coeficientes de $x$ quanto os coeficientes de $y$ nas duas equações são de valores absolutos diferentes.

Somar diretamente as equações não vai eliminar variável alguma.

Antes de aplicarmos o método da adição, precisamos escolher qual da variáveis queremos eliminar.

Vamos eliminar aqui a variável $x$. Os coeficientes de $x$ nas equações são 3 e 2.

Em seguida, encontramos o mínimo múltiplo comum de 3 e 2, que é 6.

Assim, vamos multiplicar a 1º equação por 2 e a segunda equação por $-3$, para obter

$$\left\{\begin{array}{l}
6x-4y=2 \\
-6x-15y=-21.
\end{array}\right. $$

Agora é só seguir o passo a passo acima do método da adição.

Método da Comparação

O método da comparação consiste em isolar a mesma variável tanto na 1ª equação quanto na 2ª e igualar os valores isolados.

Vamos ver como resolver um sistema usando esse método passo a passo.

Considere o seguinte sistema:

$$\left\{\begin{array}{l}
6x-2y=4 \\
5x+y=14.
\end{array}\right. $$

1º passo: Escolha uma variável e a isole em ambas as equações.

Fazendo isso no nosso caso, obtemos

$$\left\{\begin{array}{l}
y=\dfrac{4-6x}{-2}=3x-2 \\
y=14-5x.
\end{array}\right. $$

2º passo: Iguale as expressões encontradas para obter uma equação do 1º grau em uma variável.

Igualando as expressões, obtemos $$3x-2=14-5x.$$
3º passo: Resolva essa equação. Vamos resolver a equação $$3x-2=14-5x\Rightarrow 8x=16\Rightarrow x=2.$$
4º passo: Substitua o valor encontrado em uma das equações e encontre o valor da outra variável.

Substituindo $x=2$ na 1ª equação de

$$\left\{\begin{array}{l}
y=3x-2 \\
y=14-5x.
\end{array}\right. $$

obtemos $$y=3\cdot 2-2=4.$$

5º passo: Faça a verificação.

Substituindo $x=2$ e $y=4$ em

$$\left\{\begin{array}{l}
6x-2y=4 \\
5x+y=14.
\end{array}\right. ,$$

temos $$6\cdot 2-2\cdot 4=12-8=4$$ e $$5\cdot 2+4=10+4=14.$$

Portanto, a solução desse sistema é o par $(2,4)$.

Como resolver problemas usando sistemas de equações do 1º grau?

Alguns problemas matemáticos podem ser resolvidos usando sistemas de equações de 1º grau com duas variáveis.

Vamos ver alguns exemplos e vejamos como resolvê-los.

Problema 1

(FEC) No almoxarifado de uma empresa há canetas e borrachas num total de 305
unidades.

Se o número de canetas é igual ao triplo do número de borrachas diminuído
de 35 unidades, o número de canetas é:
a) 160.
b) 190.
c) 200.
d) 220.
e) 250.
Solução

Para resolver problemas desse tipo, vamos seguir os seguintes passos.

Passo 1: Identifique os valores desconhecidos e chame-os de $x$ e $y$.

Nesse problema, os valores desconhecidos são

• o número de canetas que vamos chamar de $x$;
• o número de borrachas que vamos chamar de $y$.

Passo 2: Identifique a relação entre as quantidades desconhecidas.

Segundo os dados do problema, no almoxarifado da empresa há canetas e borrachas num total de 305 unidades.

Assim, essa relação é expressa por $$x+y=305.$$

Passo 3: Expresse as condições do problema em termos de $x$ e $y$.

A condição aqui é que o número de canetas seja igual ao triplo do número de borrachas diminuído de 35 unidades.

Ou seja, $$x=3y-35.$$

Passo 4: Monte e resolva o sistema.

O sistema formado pelas duas equações encontradas é

$$\left\{\begin{array}{l}
x+y=305 \\
x=3y-35.
\end{array}\right. $$

Para resolver esse sistema, usamos um dos métodos vistos anteriormente.

Vamos usar aqui o método da substituição.

Como $x=3y-35$, substituímos isso na 1ª equação para obter $$3y-35+y=305\Rightarrow 4y=340,$$ o que implica $$y=85.$$ Ou seja, o número de borrachas é de 85 unidades.

Para encontrar $x$, vamos usar a equação $x=3y-35$. Substituindo $y=85$, obtemos $$x=3\cdot 85-35=220.$$

Portanto, o número de canetas é 220 e a alternativa correta é a d).

Problema 2

Em um número de dois algarismos, o algarismo das unidades é três vezes o algarismo das dezenas.

Se 36 for adicionado ao número, os algarismos trocam de lugar. Encontre o número.

Solução

Vamos seguir o passo a passo acima para resolver esse problema.

Vamos chamar de $x$ o algarismo das unidades e de $y$ das dezenas.

A relação entre $x$ e $y$ é $$x=3y.$$

Alem disso, somando 36 a esse número, os algarismos trocam de lugar. Ou seja, $$10y+x+36=10x+y,$$ ou seja, $$9x-9y=36\Rightarrow x-y=4.$$

Assim, chegamos ao sistema

$$\left\{\begin{array}{l}
x=3y\\
x-y=4.
\end{array}\right. $$

Substituindo $x=3y$ na 2ª equação, obtemos $$3y-y=4\Rightarrow 2y=4\Rightarrow y=2.$$

Como $x=3y$, segue que $x=6$.

Portanto, o número procurado é 26.

Verificando: De fato,$$6=3\cdot 2$$ e $$26+36=62.$$

Conclusão

Aprender resolver sistemas de equações do 1º grau requer prática de vários exercícios e problemas.

Com o que você viu aqui, você saberá quantas soluções um sistema terá só de olhar para ele.

Ou seja, você será capaz de dizer se ele é

• possível e determinado;
• possível e indeterminado ou
• impossível.

Além disso, com os métodos

• da substituição;
• da adição
• e da comparação

você será capaz de lidar com qualquer sistema de equações do 1º grau com duas variáveis daqui para frente.

Finalmente, eu acredito que se você seguir o passo a passo de

1. Identificar os valores desconhecidos e chamá-los de $x$ e $y$
2. Identificar qual a relação entre eles
3. E expressar as condições o problema em termos de $x$ e $y$

você irá melhorar na resolução de questões em que você precisar interpretar os enunciados.

Se você gostou desse conteúdo, compartilhe esse conhecimento com outras pessoas para ajudá-las também.