Saber como interpretar questões de matemática é um desafio para você?
Compreender um problema é uma etapa fundamental para resolvê-lo.
Não tem como resolver algo que não se compreende.
É como querer fazer uma viagem e não saber o destino.
Para entender um problema, você precisa antes conhecer os elementos que o constituem.
Uma vez entendidos esses elementos você saberá quais as ações serão tomadas ao longo da resolução.
Se você quer saber como interpretar questões de matemática, continue lendo esse artigo que eu vou te mostrar 4 passos simples para você entender um problema.
Mas antes disso, eu preciso te explicar o que é um problema e quais seus principais elementos.

O que é um problema?
Um problema é uma questão que oferece dificuldade a alguém que se propõe a resolvê-lo.
É uma situação na qual se requer a descoberta de informações matemáticas desconhecidas (problemas de determinação) ou a criação de uma demonstração para um determinado fato matemático que foi proposto (problemas de demonstração).
Exemplo 1: Doze colegas de trabalho saem para almoçar
juntos e pedem três pizzas. Cada pizza é cortada
em oito fatias. Se cada pessoa obtiver o mesmo número
de fatias, quantas fatias cada pessoa receberá?
Esse exemplo mostra um problema de determinação, pois ele pede para determinar o número de fatias que cada pessoa vai receber.
Exemplo 2: Seja $ABC$ um triângulo retângulo em $B$. Sejam $a=\overline{AC}$, $b=\overline{AB}$ e $c=\overline{BC}$. Mostre que $$a^2=b^2+c^2.$$
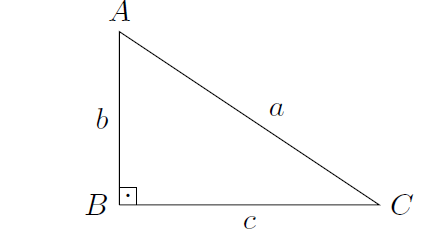
Já esse exemplo, é de um problema de demonstração que pede para demonstrar o Teorema de Pitágoras.
Componentes de um problema matemático
Em um problema, existem três componentes essenciais
que devemos prestar atenção, que são
- dados;
- operações;
- objetivo.
Dados
Os dados são informações que você vai usar para resolver
o problema.
Algumas dessas informações estarão explícitas no enunciado e outras implícitas, de modo que você pode descobri-las olhando para as propriedades dos objetos envolvidos nos dados do problema.
Não se preocupe, mais adiante irei te mostrar um exemplo identificando esses componentes na prática.
Operações
As operações são ações permitidas que você executa sobre
os dados do problema ou sobre expressões derivadas desses dados.
São os passos que você dá para sair dos dados e ir até o objetivo.
Em geral são as operações conhecidas da Matemática e da lógica.
Objetivo
O objetivo é a expressão final aonde se pretender chegar.
Como te prometi, irei te mostrar agora o exemplo no qual se fará a identificação desses componentes.
Exemplo
Considere o seguinte problema:
O perímetro de um triângulo é 12 cm e as medidas dos lados são números consecutivos. Qual a medida do lado menor?
Quais são os dados do problema? Os dados que estão
dados explicitamente são
- o perímetro do triângulo é 12 cm
- As medidas dos lados são números consecutivos
Já os dados implícitos são
- um triângulo tem três lados;
- o perímetro de um triângulo é a soma das medidas
dos seus lados.
Agora, quais são as operações? Quais acões precisam
ser executadas para se resolver o problema?
Bom, as operações que eu faria seriam as seguintes
- chamar de $x$ o valor desconhecido;
- usar os dados e montar a equação $x + (x + 1) +(x + 2) = 12$;
- somar os termos semelhantes, obtendo $3x + 3 = 12$;
- subtrair 3 de ambos os lados, ficando com $3x = 9$;
- dividir ambos os membros da equação por 3,
chegando a $x = 3$.
E finalmente o objetivo é achar a medida do lado menor
que como vimos acima é 3 cm.
Agora que você já conhece o que é um problema e seus componentes, vamos ver os passos de como interpretar questões de matemática.
1º passo: leia o problema
Como você viu acima, um problema não consiste apenas de fórmulas e números mas também de palavras. Portanto, ler é um passo necessário para interpretar uma questão.
Assim, primeiro você deve fazer uma leitura geral da questão.
Leia somente!
A dificuldade em entender os problemas de matemática é causada pelo mito de que para estudar matemática não é preciso ler.
Se você tiver um hábito de leitura, você terá, naturalmente, maior facilidade para entender um problema.
Muitos problemas de matemática possuem enunciados enormes, como as do Enem, vestibulares e concursos, por exemplo.
Portanto, se você possui o hábito da leitura é de grande ajuda nesse casos.
Além disso, procure identificar palavras chaves que vão te ajudar a escrever as expressões matemáticas.
Você precisa estar atento a palavras como
- metade,
- dobro,
- triplo…,
além de preposições como “da”, “de” e “do” que indicam a operação de multiplicação.
Sem sombra de dúvidas, saber o significado das palavras é importante para quem quer interpretar uma questão de matemática.
Mas não basta somente isso!
É preciso saber também o contexto no qual a palavra chave está inserida, pois isso pode mudar o seu significado.
2º passo: releia o problema, fazendo uma organização dos dados
Uma vez feita a leitura geral do problema, você vai agora relê-lo
com intuito de entendê-lo e planejar a sua resolução.
Aqui de fato começa o processo da interpretação.
Para isso você vai precisar identificar os dados. Nesse etapa você pode organizá-los em uma lista, agrupá-los ou simplesmente sublinha-los.
Problemas com grandes quantidades de dados são comuns e pode causar confusão em um primeiro momento.
Assim organizar seus dados é uma estratégia bem-vinda nessa hora, pois você irá decidir quais os dados você irá utilizar.
Fazer essa organização vai te ajudar a compreender a questão.
Além disso, você terá os melhores caminhos a serem seguidos e até mesmo te dá ideias para resolve-la.
Vamos ver um exemplo.
Um fazendeiro possui galinhas e coelhos. Esses animais juntos têm 50 cabeças e 140 pés. Quantas galinhas e quantos coelhos tem o fazendeiro?
Podemos fazer uma tabela para organizar os dados dessa questão para entendermos melhor.
Os dados explicitados são o número de cabeças e o número de pés dos animais juntos.
Mas há informações/dados que são importante aqui mas que estão implícitos, a saber, uma galinha tem dois pés e um coelho tem quatro.
3º passo: faça uma figura
Dependendo do problema, esse passo pode ser usado no lugar do anterior ou complementá-lo.
Digamos que você leu o problema, uma, duas ou até três vezes, e a situação não está muito clara.
Você não consegue enxergar um caminho.
É como se você estivesse perdido no meio de um nevoeiro… O que fazer? Como clarear a situação?
Você já passou por essa situação?
Bom, é aí que fazer uma figura pode te ajudar.
Pode ser um desenho, um diagrama ou um gráfico.
Fazer uma figura, em alguns casos, ajuda a entender melhor a estrutura do problema, organizar e assimilar os dados dele, trazendo à tona informações importantes que estavam nas entrelinhas
Você pode analisar de forma simplificada a estrutura do problema e olhar para ele de uma forma mais concreta.
É o raio de luz que você precisa no meio da densa névoa da abstração.
Veja a seguir como fazer uma figura pode te deixar mais confortável na hora de interpretar uma questão de matemática.
Exemplo: No quintal de José tem três cactos: Figueira da Índia, Barril Dourado e Saguaro. A Figueira da Índia tem 1,80 m de altura. O cacto Barril Dourado tem 0,90 m a menos do que altura da Figueira da Índia. Já o Saguaro tem 1,80 m a mais de altura do que o Barril Dourado. Quais as alturas dos três cactos?
Com um pouco de raciocínio você é capaz de resolver essa questão.
Mas se fizermos figuras será mais fácil de visualizar a estrutura do problema.
Como já sabemos a altura do cacto Figueira da Índia, vamos fazer uma figura para ilustrá-lo primeiro.
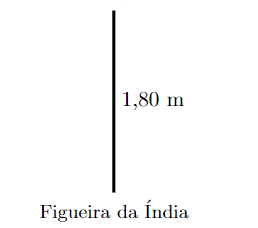
A altura do Barril Dourado é 0,90 m a menos da altura da Figueira da Índia.

Por fim, Saguaro é 1,80 m mais alto do que o Barril Dourado.
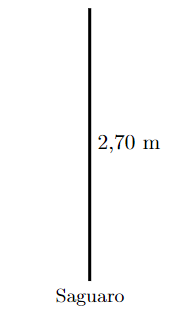
A partir das figuras você consegue visualizar a situação e calcular as alturas dos cactos tranquilamente, que são 1, 80 m, 0,90 m e 2,70 m respectivamente.
4º passo: identifique o objetivo do problema
Quando você for compreender um problema, a primeira pergunta que você tem que fazer é : “o que queremos?” ou “o que a questão está pedindo?” ou ainda “qual o objetivo desse problema”.
Para poder identificar o objetivo do problema, você precisa saber com qual tipo de problema você está lidando.
Basicamente existem dois tipos de problemas:
- Problemas de determinação;
- Problemas de demonstração.
Os problemas de determinação são aqueles nos quais se pede para determinar algo, ou seja, achar um valor.
E esse é justamente o objetivo dos problemas de determinação: achar o valor ou a expressão final.
Geralmente esses problemas terminam com uma pergunta ou com uma frase no imperativo começando com uma das palavras: determine, calcule, ache, encontre… Aqui o objetivo está especificado, mas não de forma explícita.
Exemplo: A soma de dois números é 84 e a diferença é 12. Quais são esses números?
O objetivo nesse problema é achar esses números.
Já para resolver problemas de demonstração é preciso provar uma afirmação, ou seja, mostrar através de uma sequência de argumentos válidos que a sentença é verdadeira.
Nesse caso, o objetivo está completamente especificado no problema.
Esse tipo de problema termina com uma frase começando com “Mostre que” ou “Prove que”.
Exemplo: Prove que $\sqrt{3}$ é irracional.
Observe que o objetivo está completamente especificado: concluir que $\sqrt{3}$ é um número irracional.
Assim, quando você terminar de interpretar a questão você precisa saber claramente qual o objetivo, ou seja, aonde você quer chegar.
Conclusão
Os problemas de matemática estarão bem presentes na sua vida ao longo da sua jornada como estudante.
Por isso, você precisa está preparado para interpretar esses problemas e resolvê-los.
Nesse artigo, você viu o que é um problema e seus principais componentes como também alguns passos que podem te ajudar na hora de interpretar um problema de matemática:
- ler;
- reler organizando os dados;
- fazer uma figura;
- identificar o objetivo do problema.
Espero que você tenha gostado desse conteúdo e ponha em prática essas estratégias nas próximas questões que for resolver.




0 Comentários