Área do setor circular: como calcular

Você já se deparou com situações em que precisa calcular a área de uma parte de um círculo, como uma fatia de pizza ou o setor de um gráfico?

Se sim, saiba que entender como calcular a área de um setor circular é essencial para resolver problemas do dia a dia em diversas áreas.

Neste artigo, vamos simplificar o cálculo da área de um setor circular.

Vamos explicar a fórmula, detalhar os conceitos envolvidos e apresentar exemplos práticos, tudo de forma clara e objetiva, para que você possa aplicar esse conhecimento facilmente.

Ao longo deste post, você aprenderá o que é um setor circular, como calcular sua área passo a passo e verá exemplos reais de aplicação.

No final, estará pronto para resolver qualquer problema envolvendo áreas de setores circulares de maneira rápida e eficiente!

O que é um setor circular

Um setor circular é uma região do círculo limitada por dois raios e o arco entre eles.

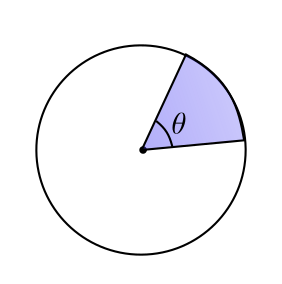
Imagine um pedaço de pizza: a borda arredondada corresponde ao arco do setor, e as duas laterais do pedaço são os raios.

Mais formalmente, um setor circular é definido por um ângulo central, que é o ângulo formado entre os dois raios que partem do centro do círculo até a borda.

Esse ângulo central pode variar de 0° (sem área) a 360° (o círculo completo). O tamanho do setor depende diretamente do valor desse ângulo: quanto maior o ângulo, maior será a área do setor.

Como calcular a área de um setor circular.

Lembre que a área do círculo é dada por $$A=\pi r^2.$$
Agora, observe que quando dobrarmos o arco, dobramos a área do setor. Se triplicarmos o arco, triplicamos a área do setor e assim por diante.

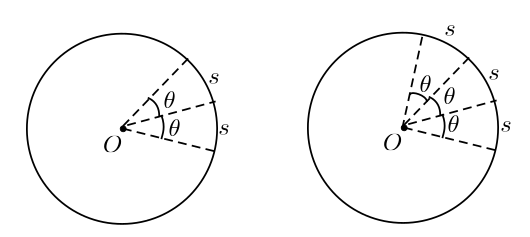
Ou seja, a área do setor é diretamente proporcional ao comprimento do arco.

Assim, podemos calcular a área do setor circular através de uma regra de três simples.

Sejam $\theta$ a medida do ângulo central do setor, em radianos, e $r$ o raio do setor.

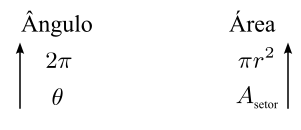
Temos $$\frac{2\pi }{\theta }=\frac{\pi r^2}{A_{\text{setor}}}\Rightarrow 2\pi A_{\text{setor}}=\pi r^2\theta \Rightarrow A_{\text{setor}}=\frac{1}{2}{r}^2\theta .$$
Se as medidas forem dadas em graus, temos $$\frac{360°}{\theta }=\frac{\pi r^2}{A_{\text{setor}}}\Rightarrow A_{\text{setor}}=\frac{\pi r^2\theta }{360°}.$$

Exemplos

Exemplo 1: Encontre a área de um setor circular se o raio do círculo for 12 cm e o ângulo central for $\theta ={\displaystyle \frac{2\pi }{3}}$.

Usando a primeira fórmula, temos que $$A=\frac{1}{2}\cdot {12}^2\cdot \frac{2\pi }{3}=48\pi {\mathrm{c}\mathrm{m}}^2.$$

Exemplo 2: Considere um círculo com raio $r=10$ cm e um ângulo central $\theta =60°$. A área do setor circular será $$A=\frac{\pi \cdot {10}^2\cdot 60°}{360°}=\frac{100\pi }{6}{\mathrm{c}\mathrm{m}}^2.$$

Com o que foi abordado neste artigo, você está preparado para calcular áreas de setores circulares.

Agora, é hora de colocar o conhecimento em prática e explorar os diferentes contextos em que ele pode ser útil!