Qual o significado geométrico da derivada?
Que relação existe entre o gráfico de uma função e sua derivada?
Ao entender essa relação, como posso usar isso para resolver certos problemas de Cálculo?

Esses problemas de Cálculo a que me refiro são aqueles que envolvem retas tangentes a gráficos de funções.
Se você quer obter as repostas a essas perguntas, basta continuar lendo esse artigo.
O que é a derivada de uma função
Para entender qual o significado geométrico da derivada precisamos relembrar o que é a derivada de uma função em um ponto.
Seja $f$ uma função definida em um intervalo aberto contendo o ponto $a\in\mathbb{R}$.
Dizemos que $f$ é diferenciável em $a$ se existe o limite \[f'(a)=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=\lim_{h\to 0}\frac{f(a+h)-f(a)}{h}.\]
O número $f'(a)$ é chamado de derivada de $f$ no ponto $x=a$.
Agora que você já lembrou da definição da derivada, já está pronto para entender o seu significado geométrico.
Interpretação geométrica da derivada
Fixe o ponto $P=(a,f(a))$ no gráfico de $f$ como mostra a figura abaixo.
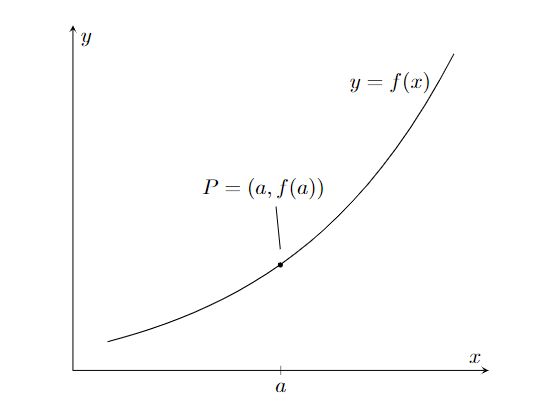
Para cada $x\in\mbox{dom}(f)$ e $x\neq a$, consideramos o ponto $Q=(x, f(x))$. A reta secante que passa pelos pontos $P$ e $Q$ tem inclinação igual a \[\frac{\Delta f}{\Delta x}=\frac{f(x)-f(a)}{x-a}.\]
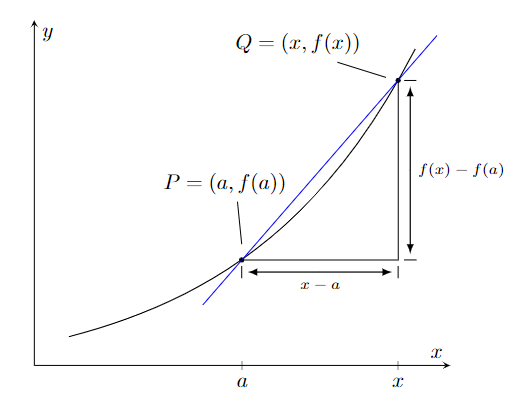
Lembre que a inclinação $m$ de uma reta que faz um ângulo $\alpha$ com o eixo $Ox$ pode ser dada por \[m=\tan\alpha.\]
Observe que quando $x$ se aproxima de $a$, o ponto $Q$ se aproxima de $P$.
Dessa forma as retas secantes correspondentes vão aos poucos se aproximando da reta tangente ao gráfico de $f$ no ponto $P$.
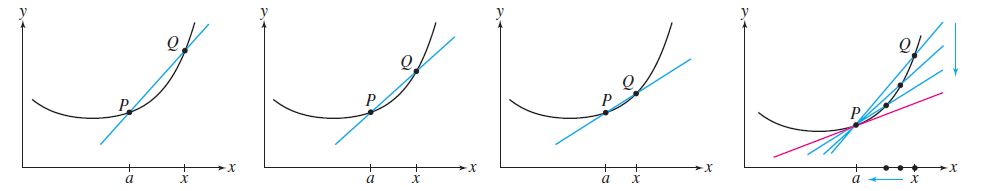
Assim, é natural que a inclinação dessa reta tangente seja o limite das inclinações das retas secantes.
Em outras palavras, \[\tan\alpha=\lim_{x\to a}\frac{f(x)-f(a)}{x-a}=f'(a).\]
Ou seja, a derivada de $f$ no ponto $a$ é a inclinação da reta tangente ao gráfico de $f$ no ponto $P=(a,f(a))$.
Esse é o significado geométrico da derivada.
Equação da reta tangente
Agora que você sabe que a derivada de uma função $f$ em um ponto $x=a$ é a inclinação da reta tangente ao seu gráfico em $(a,f(a))$, você será capaz de como encontrar a equação dessa reta tangente.
Para deduzir essa equação, lembre que a equação reduzida de uma reta é da forma \[y=mx+b.\]
No nosso caso da reta tangente, sabemos duas coisas
- $m=f'(a)$ e
- o ponto $(a, f(a))$ pertence a reta.
O segundo item acima nos dá o valor de $b$.
De fato, quando $x=a$, $y=f(a)$ e com isso, \[b=f(a)-ma=f(a)-f'(a)a.\]
Dessa forma, a equação $y=mx+b$ se transforma em \[y=f'(a)x+(f(a)-f'(a)a)=f'(a)(x-a)+f(a),\] ou \[y-f(a)=f'(a)(x-a).\]
Problemas envolvendo o significado geométrico da derivada
Problema 1: Suponha que a reta tangente ao gráfico de uma função $f$ em $x=1$ passa pelo ponto $(4,9)$ e que $f(1)=3$. Qual o valor de $f'(1)$?
Solução.
Como vimos acima, $f'(1)$ é a inclinação da reta tangente ao gráfico de $f$ em $x=1$.
Sabemos pelo enunciado que essa reta passa pelo ponto $(4,9)$.
Além disso, uma vez que a reta é tangente ao gráfico em $x=1$ e $f(1)=3$, concluímos que a reta também passa pelo ponto $(1,3)$.
Ora, conhecendo dois pontos por onde uma reta passa, é possível determinar a sua inclinação.
De fato, se uma reta passa pelos pontos $(x_1,y_1)$ e $(x_2,y_2)$, então sua inclinação é dada por \[m=\frac{y_2-y_1}{x_2-x_1}.\]
Como os pontos por onde a reta em questão passa são $(1,3)$ e $(4,9)$, segue que \[f'(1)=\frac{9-3}{4-1}=\frac{6}{3}=2.\]
Problema 2: Encontre a área delimitada pela parábola $y=x^2$, pela reta tangente à parábola no ponto $(2,4)$ e pelo eixo $Ox$.
Solução.
Primeiro vamos encontrar a equação da reta tangente mencionada no enunciado.
Seja $f(x)=x^2$.
A derivada de $f$ é $f'(x)=2x.$
A inclinação da reta tangente ao gráfico de $f$ em $(2,4)$ é $f'(2)=4$.
Portanto, a equação dessa reta é $y-f(2)=f'(2)(x-2)$, ou seja, \[y-4=4(x-2)\Rightarrow y=4x-4.\]
A situação está ilustrada a seguir.
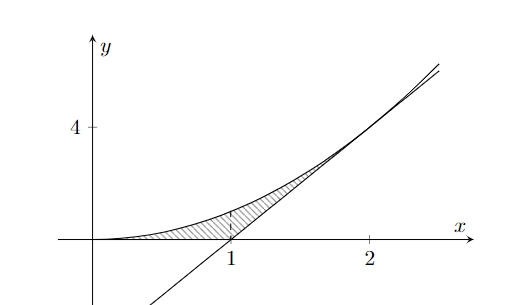
Observe que dividimos a região em duas.
E vamos calcular a área de cada uma delas usando integrais.
A área da região à esquerda é igual a \[\int_0^1x^2\;dx=\frac{x^3}{3}\Big|_0^1=\frac{1}{3}.\]
E a área da outra região é igual
\begin{eqnarray*}
\int_1^2[x^2-(4x-4)]\;dx&=&\int_1^2(x^2-4x+4)\;dx\\
&=&\left(\frac{x^3}{3}-2x^2+4x\right)\Big|_1^2\\
&=&\frac{8}{3}-8+8-\left(\frac{1}{3}-2+4\right)\\
&=&\frac{7}{3}-2\\
&=&\frac{1}{3}.
\end{eqnarray*}
Portanto, a área da região é \[\frac{1}{3}+\frac{1}{3}=\frac{2}{3}.\]
Espero que esse conteúdo tenha te ajudado a entender melhor sobre a derivada de uma função.
Até a próxima!


0 Comentários