Você já ouviu falar em cevianas de um triângulo?
Esses segmentos de reta são bastante importantes na geometria, pois ajudam a entender muitas propriedades de um triângulo.
As cevianas são definidas como segmentos de reta que conectam um vértice do triângulo a um ponto qualquer da reta que contém o lado oposto.
Elas surgem como elementos-chave, desempenhando um papel crucial na compreensão das propriedades e interconexões dentro do triângulo.
O estudo desses segmentos de reta não apenas amplia nossa percepção geométrica, mas também fornece ferramentas essenciais para desvendar uma gama diversificada de problemas matemáticos.
Se você está estudando geometria ou simplesmente quer aprender mais sobre triângulos, é fundamental entender o que são as cevianas e como elas funcionam.
Este guia abrangente busca oferecer uma visão clara e acessível das cevianas, permitindo que leitores de todos os níveis de familiaridade com a geometria desfrutem e compreendam sua importância dentro desse reino matemático.
Definição de Cevianas
Uma ceviana é um segmento de reta que conecta um vértice de um triângulo a qualquer ponto da reta que contém o lado oposto.
Assim, se $X$, $Y$ e $Z$ são pontos pertencentes aos respectivos lados $BC$, $AC$, $AB$ do triângulo $ABC$, os segmentos $AX$, $BY$, $CZ$ são cevianas.
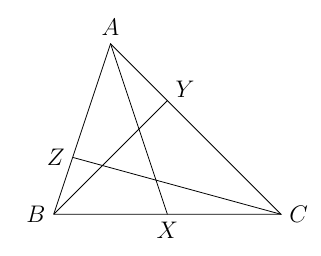
Esse termo vem do nome do matemático italiano Giovanni Ceva.
Ao entendermos as cevianas, ganhamos uma ferramenta valiosa para desvendar aspectos da geometria, permitindo não apenas a compreensão da estrutura do triângulo, mas também sua aplicação em problemas matemáticos diversos.
Cevianas Especiais
Existem cevianas especiais que são estudadas com frequência na geometria:
- medianas,
- alturas e
- bissetrizes.
Medianas
Uma mediana é uma ceviana que que conecta um vértice de um triângulo ao ponto médio do seu lado oposto.
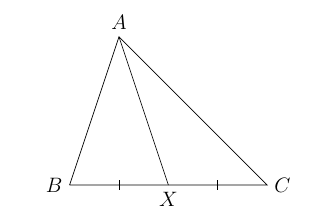
Cada triângulo possui três medianas. Além disso, mostraremos mais adiante que esses três segmentos se intersectam em um ponto, chamado de baricentro.
Alturas
Uma altura é uma ceviana que conecta um vértice do triângulo ao lado oposto, formando um ângulo reto.
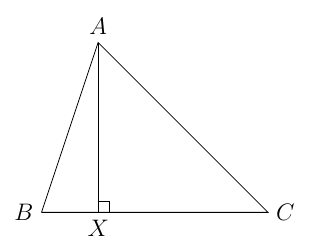
Cada triângulo possui três alturas que se encontram no ortocentro do triângulo.
Bissetrizes
Uma bissetriz é uma ceviana que divide o ângulo de um vértice em duas partes iguais.
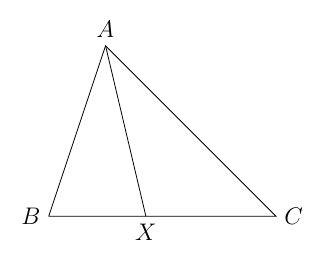
Cada triângulo possui três bissetrizes que se encontram no incentro do triângulo.
Teorema de Ceva
Em 1678, Ceva publicou uma condição necessária e suficiente para a concorrência de três cevianas, uma de cada vértice.
Apresentamos o seu resultado a seguir.
Teorema de Ceva: Seja $ABC$ um triângulo com pontos $X, Y$ e $Z$ nos lados $BC, AC$ e $AB$, respectivamente. Então as cevianas $AX, BY, CZ$ são concorrentes se e somente se $$\frac{\overline{BX}}{\overline{XC}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot\frac{\overline{AZ}}{\overline{ZB}}=1.$$
Demonstração: Mostraremos primeiro que se as cevianas são concorrentes então
$$\frac{\overline{BX}}{\overline{XC}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot\frac{\overline{AZ}}{\overline{ZB}}=1.$$
Denote por $P$ o ponto de interseção das três cevianas e escreva $S_{ABC}$ para denotar a área do triângulo $ABC$.
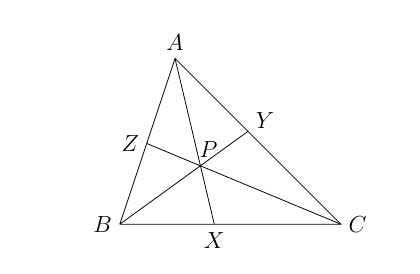
Note que os triângulos $BXP$ e $CXP$ possuem a mesma altura $h_1$, com relação às bases $BX$ e $XC$, respectivamente.
E os triângulos $ABX$ e $ACX$ têm altura $h_2$ com respeito às bases $BX$ e $CX$, respectivamente.
Dessa forma, $$S_{ABX}=\frac{\overline{BX}\cdot h_2}{2},\quad S_{ACX}=\frac{\overline{CX}\cdot h_2}{2}$$ e $$S_{BXP}=\frac{\overline{BX}\cdot h_1}{2}\quad\mbox{e}\quad S_{CXP}=\frac{\overline{CX}\cdot h_1}{2}.$$
Daí, segue que
$$\frac{S_{ABP}}{S_{ACP}}= \frac{S_{ABX}-S_{BXP}}{S_{ACX}-S_{CXP}} = \frac{\frac{\overline{BX}\cdot h_2}{2}-\frac{\overline{BX}\cdot h_1}{2}}{\frac{\overline{CX}\cdot h_2}{2}-\frac{\overline{CX}\cdot h_1}{2}}= \frac{\overline{BX}}{\overline{CX}}.$$
Portanto, $$\frac{\overline{BX}}{\overline{CX}}=\frac{S_{ABP}}{S_{ACP}}.$$
Similarmente, obtemos $$\frac{\overline{CY}}{\overline{YA}}=\frac{S_{BCP}}{S_{ABP}}\quad\mbox{e}\quad \frac{\overline{AZ}}{\overline{ZB}}=\frac{S_{CAP}}{S_{BCP}}.$$
Assim,
$$\frac{\overline{BX}}{\overline{CX}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot \frac{\overline{AZ}}{\overline{ZB}}=\frac{S_{ABP}}{S_{ACP}}\cdot\frac{S_{BCP}}{S_{ABP}}\cdot \frac{S_{CAP}}{S_{BCP}}=1.$$
Mostremos agora a recíproca, ou seja, se vale $$\frac{\overline{BX}}{\overline{XC}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot\frac{\overline{AZ}}{\overline{ZB}}=1,$$ então as cevianas $AX, BY, CZ$ são concorrentes.
Seja $P$ o ponto de encontro das cevianas $AX$ e $BY$. Vamos mostrar que $CZ$ passa por $P$.
Seja $CZ’$ uma ceviana que passa por $P$. Pela primeira parte do Teorema, temos $$\frac{\overline{BX}}{\overline{XC}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot\frac{\overline{AZ’}}{\overline{Z’B}}=1,$$
Por hipótese, obtemos $$
\frac{\overline{AZ’}}{\overline{Z’B}}=\frac{\overline{AZ}}{\overline{ZB}}.$$
Afirmamos que $Z’=Z$. De fato, se tivéssemos $Z’\neq Z$, então teríamos $\overline{AZ}>\overline{AZ’}$ ou $\overline{AZ}<\overline{AZ’}$.
Suponha sem perda de generalidade que $\overline{AZ}>\overline{AZ’}$. Então teríamos $\overline{ZB}<\overline{Z’B}$, ou seja, $\dfrac{1}{\overline{ZB}}>\dfrac{1}{\overline{Z’B}}$. Com isso temos
\begin{align*} \frac{\overline{AZ’}}{\overline{Z’B}}< \frac{\overline{AZ'}}{\overline{ZB}}<\frac{\overline{AZ}}{\overline{ZB}} \end{align*}
o que é uma contradição.
Portanto, $Z’=Z$ como afirmado anteriormente.
Consequências do Teorema de Ceva
Vejamos agora algumas consequências do Teorema de Ceva.
Corolário: As medianas de um triângulo são concorrentes.
Demonstração: Considere um triângulo $ABC$ e sejam $X, Y$ e $Z$ os respectivos pontos médios de $BC, AC$ e $AB$.
Com isso, temos $$\frac{\overline{BX}}{\overline{XC}}\cdot\frac{\overline{CY}}{\overline{YA}}\cdot\frac{\overline{AZ}}{\overline{ZB}}=1\cdot1\cdot 1=1,$$ e o resultado segue pelo Teorema de Ceva.
Teorema: As medianas de um triângulo o divide em seis triângulos de mesma área.
Demonstração:
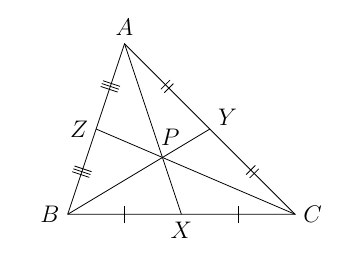
Note que
- $S_{BPX}=S_{CPX}$
- $S_{BPZ}=S_{APZ}$
- $S_{CPY}=S_{APY}$,
pois têm a mesma altura com respeito a base congruentes. Além disso, temos $S_{AXC}=S_{ABX}$ pela mesma razão.
Por outro lado, temos $$S_{AXC}=S_{APY}+S_{CPY}+S_{CPX}=2S_{APY}+S_{CPX}$$
e $$S_{ABX}=S_{APZ}+S_{BPZ}+S_{BPX}=2S_{APZ}+S_{CPX}.$$
Daí e de $S_{AXC}=S_{ABX}$, segue que $$S_{APY}=S_{APZ}.$$ Analogamente, mostramos que $S_{APY}=S_{BPX}$.
Teorema: O ponto de interseção das medianas as divide na razão 2 para 1.
Demonstração: Segue do teorema anterior que $S_{APB}=2S_{PBX}$.
Além disso, os triângulos $APB$ e $PBX$ têm a mesma altura $h$ com relação às bases $AP$ e $PX$.
Por isso, $$S_{APB}=\frac{\overline{AP}\cdot h}{2}$$ e $$S_{PBX}=\frac{\overline{PX}\cdot h}{2},$$ donde segue que $\overline{AP}=2\overline{PX}$. Da mesma forma, mostramos que $\overline{BP}=2\overline{PY}$ e $\overline{CP}=2\overline{PZ}$.
Conclusão
Vimos que as cevianas de um triângulo possuem diversas propriedades interessantes, mas também podem apresentar desafios e problemas na sua utilização.
A compreensão dessas propriedades e a habilidade em resolver problemas envolvendo cevianas são importantes na resolução de problemas de geometria.
Compartilhe esse texto se você gostou do conteúdo.

0 Comentários