Resolver um problema matemático, às vezes, é uma tarefa desafiadora e deixa alguns estudantes perdidos sem saber por onde começar.
Você já se sentiu assim?
Se sim, não se preocupe, esse sentimento é mais comum do que você pensa. Até os mais experientes demoram resolver problemas com nível mais elevado.
Nesse artigo eu vou te mostrar algumas perguntas importantes que precisam ser respondidas antes de resolver um problema matemático.
Essas perguntas formam um guia básico no processo de resolução de problemas. Ao fazê-las para você mesmo, você terá o que fazer, ou melhor, o que pensar, em vez de ficar encarando o problema e a folha em branco.
Se você quer saber o mínimo do que é preciso para resolver problemas matemáticos é só continuar lendo esse artigo que já vou te mostrar quais são as perguntas.

Pergunta 1: “O que eu sei?”
A primeira pergunta que você deve fazer quando for resolver um problema matemático é “O que eu sei?”.
Ao se fazer essa pergunta, você está querendo entender o problema.
Para entender melhor o que essa pergunta significa, você precisa saber que um dos elementos que constituem o problema são os dados.
Os dados são as informações que você vai usar para resolver o problema. Essas informações estão presentes no enunciado do problema.
Além disso, você pode usar também outras informações que estão implícitas, mas que estão relacionadas com as explícitas.
Por isso, você sempre deve manter a memória fresca, consultando ou revisando material contendo definições, propriedades e resultados relacionados com os objetos do enunciado.
Portanto, quando você faz a pergunta “o que eu sei?” você está fazendo a seguinte pergunta: “quais são os dados do problema?
Vamos ver alguns exemplos.
Exemplo 1
Ben se exercita a cada 12 dias e Isabel a cada 8 dias. Ben e Isabel se exercitaram hoje. Quantos dias serão necessários até que se exercitem juntos novamente?
Nesse exemplo, o que nós sabemos? Quais são os dados do problemas?
Sabemos que Ben se exercita a cada 12 dias e Isabel a cada 8 dias. Além disso, sabemos que Ben e Isabel se exercitaram hoje.
Exemplo 2
No diagrama abaixo, as retas $r$ e $s$ são paralelas, a área do triângulo $ABC$ é $10\; \textrm{cm}^2$, *e a área do triângulo *$ADC$ é $8\;\textrm{cm}^2$. Qual o valor de $$\dfrac{\small\overline{{AD}}}{\small\overline{BC}}?$$
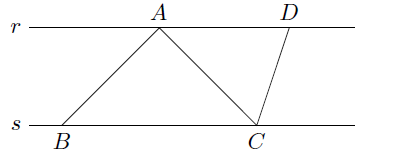
Aqui, o que nós sabemos?
Sabemos que
- as retas $r$ e $s$ são paralelas;
- o triângulo $ABC$ tem área igual a $10\;\textrm{cm}^2$ e
- o triângulo $ADC$ tem área igual a $8\;\textrm{cm}^2$.
Pergunta 2: “O que eu quero saber?”
Depois que você responde a pergunta “o que eu sei?”, você irá responder a próxima pergunta, que é ” o que eu quero saber?”.
Você ainda está no processo de entender o problema. Um outro elemento que constitui o problema é o objetivo.
O objetivo, como o nome já diz, é o aonde você quer chegar, é a determinação da resposta e o que você quer saber.
Assim, ao responder a pergunta “o que eu quero saber?” você está descobrindo qual o objetivo do problema.
Vamos voltamos aos nossos exemplos.
No primeiro exemplo, o que queremos saber?
Observe a pergunta contida no problema: Quantos dias serão necessários até que se exercitem juntos novamente?
Logo, o que queremos saber é depois de quantos dias Ben e Isabel irão se exercitar novamente. Queremos descobrir uma quantidade, um número.
Já no segundo exemplo o que queremos saber é o valor de $$\dfrac{\small\overline{{AD}}}{\small\overline{BC}}.$$
Pergunta 3: ” Qual é o meu plano?”
Agora que você já entendeu o problema, sabe o que você tem e sabe o que você quer, você agora vai pensar em como resolver o problema. Para isso você precisa de um plano de resolução.
Por isso, a terceira pergunta que você deve fazer é “qual é o meu plano?”.
É aqui que as ideias surgem.
Você vai usar as informações que você tem, fazer figuras, diagramas e listas com intuito de chegar no seu objetivo.
Um terceiro elemento essencial de um problema são as operações.
As operações são passos executados para sair dos dados e ir para o objetivo.
Assim, quando você pergunta “qual é o meu plano?”, você pergunta quais serão as operações usadas para resolver o problema.
Uma vez que você tem um plano em mente ou rascunhado, você irá executar esse plano, escrevendo com cuidado as suas argumentações, justificando cada passo dado.
É importante ressaltar que até achar um plano de resolução, você terá suado a camisa, pois esse é um processo árduo.
Lembre-se que resolver um problema é diferente de resolver um exercício de rotina.
Você terá que pensar mais, usar mais a sua criatividade e estudar caminhos possíveis.
Você errará, terá que voltar atrás e começar de novo. O processo é esse mesmo em qualquer nível em que se estude matemática.
Agora que você sabe o que lhe espera quando você estiver elaborando o seu plano, vamos ver como fazemos isso com os nossos exemplos.
Exemplo 1
Ben se exercita a cada 12 dias e Isabel a cada 8 dias. Ben e Isabel se exercitaram hoje. Quantos dias serão necessários até que se exercitem juntos novamente?
Como vimos acima, já sabemos o que temos (dados) e o que queremos saber (objetivo). Falta agora fazer um plano (quais operações executar).
Primeiro, note que para eles se encontrarem novamente, a quantidade de dias necessários deve ser um múltiplo tanto de 12 quanto de 8.
Em segundo lugar, esse múltiplo tem que ser o menor, pois a pergunta é quando eles se encontrarão novamente. Portanto, esse problema se resolve calculando o mínimo múltiplo comum de 12 e 8.
Por fim, calculamos $\textrm{mmc}(12,8)$ que é igual a 24.
Exemplo 2
No diagrama abaixo, as retas $r$ e $s$ são paralelas, a área do triângulo $ABC$ é $10\; \textrm{cm}^2$, *e a área do triângulo *$ADC$ é $8\;\textrm{cm}^2$. Qual o valor de $$\dfrac{\small\overline{{AD}}}{\small\overline{BC}}$$

Primeiro, observemos que esse problema que envolve área de triângulos.
Em segundo lugar, sabemos que para calcular a área de um triângulo basta multiplicar as medidas da base e da altura e em seguida dividir por 2.
Em terceiro lugar, observemos que os segmentos $AD$ e $BC$ são as bases dos triângulos $ADC$ e $ABC$, respectivamente. Além disso, eles possuem a mesma altura $h$.
Em quarto lugar, sabemos que as áreas dos triângulos $ADC$ e $ABC$ são $8\; \textrm{cm}^2$ e $10\; \textrm{cm}^2$, respectivamente. Por outro lado, temos que $$S_{\triangle ADC}=\frac{\small\overline{AD}\cdot h}{2}$$ e $$S_{\triangle ABC}=\frac{\small\overline{BC}\cdot h}{2}.$$
Por fim, notamos que $$\frac{\small\overline{AD}}{\small\overline{BC}}=\frac{\frac{\overline{AD}\cdot h}{2}}{\frac{\overline{BC}\cdot h}{2}}=\frac{8}{10}=\frac{4}{5},$$ o que resolve o problema.
Conclusão
Como você pôde perceber, resolver um problema matemática consiste essencialmente em se fazer três perguntas:
- “o que eu sei?”;
- ” o que eu quero saber?”;
- “qual o meu plano”?.
Você viu também que as duas primeiras perguntas fazem parte da interpretação do problema e quanto a última da resolução.
Espero que esse guia simples possa te ajudar a resolver problemas matemáticos daqui para frente.




0 Comentários